数论

[网鼎杯 2020 青龙组]you_raise_me_up（大步小步算法）

首先，我们审计题目，可以发现题目中给予了我们m、c和n的值，其中n=2**512,m则是在（2，m）之间的值，c是m^flag = c mod n

可以看出，这是一道求指标的题目，我们可以通过以下方法进行计算，已知的条件为：

2^e = c1 mod n 在这其中，除了e其余条件我们都已知，在这里，我们需要使用离散对数求解的思路：

Shanks’s Babystep-Giantstep Algorithm算法：
1、n=[ √n ]+1

2、构造两个列表

list1=[1,g,g^2,g^3,……,g^n]

list2=[h,hg^(-n),hg^(-2n),……,hg^(-n**2)]

3、在两个列表中，找到两个相同的数 g^i=hg^(-jn)

=>g^(i+jn)=h mod n

4、我们所求的e=i+jn
python库应用：

python(sympy库) x=sympy.discrete_log(n,a,g)

exp

1
2
3
4
5
6
7
8
9
10
m = 391190709124527428959489662565274039318305952172936859403855079581402770986890308469084735451207885386318986881041563704825943945069343345307381099559075
c = 6665851394203214245856789450723658632520816791621796775909766895233000234023642878786025644953797995373211308485605397024123180085924117610802485972584499
n=2**512
 
 
import gmpy2
from Crypto.Util.number import *
import sympy
x=sympy.discrete_log(n,c,m)
print(long_to_bytes(x))

救世捷径（dijstra算法）

这道题感觉跟acm的寻找最短路径一样.

txt文件中每行的前两个数字作为无向图的顶点，第三个数字是两顶点之间的距离，最后的字符串是两顶点之间的内容，将起点到终点最短路径经过的边上的内容组合起来便是flag。
单源点最短路径算法：dijstra算法。
一些想到哪是哪的tips写在这里咯：

1.一些前期的初始化和数据处理

1）初始化各点之间的距离为“无穷远”（在程序中用一个比较大的数代替这个无穷远的概念），一般可以直观地想出用27*27的二维数组存这些距离值（Python中是用list套list作为过去高级语言中二维数组的那种存在……而且要注意要初始化把list里面都放上东西才行！），之后我们就操作索引是1-26的那些元素，浪费掉位置0处的空间，但可以恰好对应顶点1-26，清晰明了~

2）按行读取题目txt文件中的内容，用的是readlines()，得到的数据形式是每行作为一个元素组成的list。然后用strip()去掉行尾的换行符’\n’，再用split(’ ‘)将每行内容按空格分割组成新的list，方便后面在程序中的调用。

3）因为在2）步中已经分割出了每行的元素，就可以用2）步中的数据去初始化1）步中27*27的list中的数据，把已知的那些两点之间的距离放入即可，具体写法见程序代码。

2.实现dijstra算法的函数

1）初始化一个长度是27，元素全是0xffff（代表距离很远）的list，用于记录当前顶点（索引与顶点序号一致是1-26）对于顶点1的最短距离。

2）初始化一个长度为27，元素全是0的list，元素值用于记录当前顶点（索引与顶点序号一致是1-26）是否已经找到了距离顶点1的最短路径，确定了最短路径就置该顶点序号对应索引值的元素为1。后面将这里元素值是1的顶点称为“已经确定的集合”。每次更新完各顶点到顶点1的距离后，找到最短的一个，将该顶点位置元素置1，该顶点就不再参与后续的遍历。

3）初始化一个长度为27，元素全是1的list，用于记录当前顶点到顶点1的最短路径的前驱顶点，用于最后回溯路径。

过程：

首先找到和顶点1直连的顶点，找到这些顶点中距离顶点1最短的一个顶点，将该顶点加入“已经确定的集合“，遍历该顶点的邻接顶点，更新顶点1到各个邻接顶点的最短距离。再找到现在与顶点1距离最短的顶点（在”已经确定的集合“中的顶点就不再遍历），再去遍历该顶点的邻接顶点，更新顶点1到这些邻接顶点的最短距离，从中找到距离最短的顶点加入“已经确定的集合”，再遍历该顶点的邻接顶点，更新这些顶点与顶点1的最短距离，找到与顶点1距离最短的顶点……以此循环直至所有顶点都加入“确定的集合”。

核心思想：

每次循环都找到当前距离顶点1最近的一个顶点，判断路径中经过该顶点后再到达与其邻接的其他顶点的距离，是否比之前存储的这些顶点到顶点1的距离更短，如果更短就更新对应顶点到顶点1的最短距离，更新完后再找到与顶点1距离最短的顶点重复上述操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
graph=[]
for i in range(27):
    graph.append([]) #在一个list中放27个list，索引0-26
for i in range(27):
    for j in range(27):
        graph[i].append(0xffff) #先将图中各个顶点之间的距离初始化为一个比较大的数
f=open('./Downloads/dij.txt','r').readlines()  #按行读取，每行内容是list中的一个元素，全部内容组成一个整体的list
#这里需要先手动将txt文件中的最后一行换行去掉否则会多一个'\n'
#print(f)
li=[]
for x in f:
    li.append(x.strip().split(' ')) #strip()删除字符串前后空格，这里是去掉了最后的换行符'\n'，然后再按' '分割每行的每个元素，原本在同一子list中的一行元素也彼此独立出来
#print(li)
for x in li:
    graph[int(x[0])][int(x[1])]=int(x[2])
    graph[int(x[1])][int(x[0])]=int(x[2])

def try_dijstra():
    min_d=[0xffff for i in range(27)]  #记录点i到起点1的最短距离
    route=[1 for i in range(27)]  #记录前驱顶点
    isSure=[0 for i in range(27)]  #记录各点到起点距离是否已经确定
    for i in range(2,27):
        min_d[i]=graph[i][1]  #初始化一下能直连1的顶点和1的距离
    min_d[1]=0
    isSure[1]=1

    for i in range(26):
        min=0xfffff
        temp=-1
        for j in range(2,27): # 找到当前离顶点1最近的顶点加入已经确定的“顶点阵营”
            if isSure[j]==0 and min>min_d[j]:
                min=min_d[j]
                temp=j
        isSure[temp]=1
        for j in range(2,27):# 判断从顶点1开始，在经过该顶点后，再到达其邻接顶点的距离，是否比其邻接顶点原本到顶点1的距离更近，如果更近就更新最短距离
            if min_d[j]>min_d[temp]+graph[temp][j]:
                min_d[j]=min_d[temp]+graph[temp][j]
                route[j]=temp
    return (route,min_d)

route,min_d=try_dijstra()
print(min_d[26]) #最短距离
print(route) #前驱顶点

passv=[]  #存放顶点之间的“内容”（内容最后要组成flag
for i in range(27):
    passv.append([]) # 还是在一个list中放27个list
for i in range(27):
    for j in range(27):
        passv[i].append(0)  #需要将内部list中初始化出27个“位置”否则会报错索引越界
for x in li:
    passv[int(x[0])][int(x[1])]=x[3]
    passv[int(x[1])][int(x[0])]=x[3]

y=26
l=[]
while y!=1:
    print(y) #输出终点到起点的最短路径经过的顶点
    l.append(passv[y][route[y]]) #y到其前驱顶点route[y]之间的内容
    y=route[y]
print()
l=l[::-1]
for i in range(len(l)):
    print(l[i],end='')

'''
339
[1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 5, 5, 5, 4, 4, 4, 6, 6, 6, 25, 9, 11, 12, 6, 18, 22, 25]
26 25 22 12 5 2 
FLAG{WEIVKASJVLSJCHFSJVHJSDEV}
'''

[GKCTF 2021]Random（梅森算法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import random
from hashlib import md5

def get_mask():
    file = open("random.txt","w")
    for i in range(104):
        file.write(str(random.getrandbits(32))+"\n")
        file.write(str(random.getrandbits(64))+"\n")
        file.write(str(random.getrandbits(96))+"\n")
    file.close()
get_mask()
flag = md5(str(random.getrandbits(32)).encode()).hexdigest()
print(flag)

通过阅读代码，我们知道是求生成104组随机数后的卜随机数

通过算法出的随机数是伪随机数，这里用到的随机数生成函数式random.getrandbits(k)

random.getrandbits(k)

返回具有 k 个随机比特位的非负 Python 整数。 此方法随 MersenneTwister 生成器一起提供，其他一些生成器也可能将其作为 API 的可选部分提供。 在可能的情况下，getrandbits() 会启用 randrange() 来处理任意大的区间。在 3.9 版更改: 此方法现在接受零作为 k 的值。

所以这题考的其实是梅森算法，Mersenne Twister是为了解决过去伪随机生成器PRNG产生的伪随机数质量不高而生成的（传送门：梅森旋转算法）。我们了解MT19937能做生成在1<=k<=623个均匀分布的32位随机数。而真巧我们已经有624(（104+104*64/32+104*96/32）=624)个生成的随机数了，也就是说，根据已有的随机数，我们完全可以推出下面会生成的随机数

我们需要用到rendcrack库

先了解一下rendcrack

randcrack
工作原理
该生成器基于M e r s e n n e T w i s t e r MersenneTwisterMersenneTwister（梅森算法），能够生成具有优异统计特性的数字（与真正的随机数无法区分）。但是，此生成器的设计目的不是加密安全的。您不应在关键应用程序中用作加密方案的PRNG。
您可以[在维基百科上]了解有关此生成器的更多信息(https://en.wikipedia.org/wiki/Mersenne_Twister).
这个饼干的工作原理如下。
它从生成器获得前624个32位数字，并获得Mersenne Twister矩阵的最可能状态，即内部状态。从这一点来看，发电机应该与裂解器同步。
如何使用
将生成器生成的32位整数准确地输入cracker非常重要，因为它们无论如何都会生成，但如果您不请求它们，则会删除它们。 同样，您必须在出现新种子之后，或者在生成624 ∗ 32 位之后，准确地为破解程序馈电，因为每个624 ∗ 32 位数字生成器都会改变其状态，并且破解程序设计为从某个状态开始馈电。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from hashlib import md5
from randcrack import RandCrack
def foo(l,i):
    a=[]
    a.append(l[i])
    b1=l[i+1]>>32
    b2=l[i+1]&(2**32-1)
    a.append(b2)
    a.append(b1)
    b1=l[i+2]>>64
    b2=(l[i+2]&(2**64-1))>>32
    b3=l[i+2]&(2**32-1)
    a.append(b3)
    a.append(b2)
    a.append(b1)
    return a
with open(r'random.txt','r') as f:
    l=f.readlines()
l=[int(i.strip()) for i in l]
ll=[]
for i in range(0,len(l),3):
    ll+=foo(l,i)
rc=RandCrack()
for i in ll:
    rc.submit(i)
aa=rc.predict_getrandbits(32)
print(md5(str(aa).encode()).hexdigest())

脚本源于：

代码就很容易读懂了，先将我们有的随机数排列到一个列表ll中，然后挨个用RandCrack.submit()提交，最后用RandCrack.predict_getrandbits()预测下一个32位随机数，然后md5一下输出就好了

[SUCTF2019]MT（梅森算法）

考点是MT19937,也就是梅森旋转算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Random import random
from Crypto.Util import number
from flag import flag

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = transform(flag[5:-1].decode('hex')).encode('hex')
print 'transformed_flag:', transformed_flag
# transformed_flag: 641460a9e3953b1aaa21f3a2

加密原理很简单，就是通过 convert() 函数获取随机数将 flag 加密。考的题型是 逆向 extract_number函数

解题EXP：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#python2
from Crypto.Util import number

# right shift inverse
def inverse_right(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift
    return tmp


# right shift with mask inverse
def inverse_right_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift & mask
    return tmp

# left shift inverse
def inverse_left(res, shift, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift
    return tmp


# left shift with mask inverse
def inverse_left_mask(res, shift, mask, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift & mask
    return tmp


def extract_number(y):
    y = y ^ y >> 11
    y = y ^ y << 7 & 2636928640
    y = y ^ y << 15 & 4022730752
    y = y ^ y >> 18
    return y&0xffffffff

def convert(y):
    y = inverse_right(y,19)
    y = inverse_left_mask(y,17,2245263360)
    y = inverse_left_mask(y,9,2029229568)
    y = inverse_right(y,13)
    return y&0xffffffff

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message

transformed_flag = '641460a9e3953b1aaa21f3a2'
c = transformed_flag.decode('hex')
flag = transform(c)
print flag.encode('hex')

第二种解法是基于出题人的算法，使得明文通过不断的加密最后还是明文。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#python2
from Crypto.Random import random
from Crypto.Util import number

def convert(m):
    m = m ^ m >> 13
    m = m ^ m << 9 & 2029229568
    m = m ^ m << 17 & 2245263360
    m = m ^ m >> 19
    return m

def transform(message):
    assert len(message) % 4 == 0
    new_message = ''
    for i in range(len(message) / 4):
        block = message[i * 4 : i * 4 +4]
        block = number.bytes_to_long(block)
        block = convert(block)
        block = number.long_to_bytes(block, 4)
        new_message += block
    return new_message
def circle(m):
    t=m
    while True:
        x=t
        t=transform(t)
        if t==m:
            return x
transformed_flag='641460a9e3953b1aaa21f3a2'
flag = circle(transformed_flag.decode('hex')).encode('hex')
print('transformed_flag:', flag)

[De1CTF2019]xorz（重复密钥异或用汉明距离）

1
2
3
4
5
6
7
8
9
10
11
12
from itertools import *
from data import flag,plain

key=flag.strip("de1ctf{").strip("}")
assert(len(key)<38) 37
salt="WeAreDe1taTeam"
ki=cycle(key)
si=cycle(salt)
cipher = ''.join([hex(ord(p) ^ ord(next(ki)) ^ ord(next(si)))[2:].zfill(2) for p in plain])
print cipher
# output:
# 49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c

cycle函数

cycle() 函数是 Python 标准库 itertools 中的一个函数，可以在一个可迭代对象（例如列表、元组或字符串）中无限循环遍历元素。

zfill函数

返回指定长度的字符串，原字符串右对齐，前面填充0。

我们来审计代码，代码使用了p、ki、si进行了异或，未知部分有两个，flag和plain，最后输出结果是16进制的密文，salt和key都是循环使用的

salt是已知的，因此先把salt层去掉

1
2
3
4
5
6
from itertools import *
salt="WeAreDe1taTeam"
si=cycle(salt)
c = '49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c'.decode('hex')
no_salt = ''.join([chr(ord(p) ^ ord(next(si))) for p in c])
print no_salt.encode('hex')
1
no_salt =1e5d4c055104471c6f234f5501555b5a014e5d001c2a54470555064c443e235b4c0e590356542a130a4242335a47551a590a136f1d5d4d440b0956773613180b5f184015210e4f541c075a47064e5f001e2a4f711844430c473e2413011a100556153d1e4f45061441151901470a196f035b0c4443185b322e130806431d5a072a46385901555c5b550a541c1a2600564d5f054c453e32444c0a434d43182a0b1c540a55415a550a5e1b0f613a5c1f10021e56773a5a0206100852063c4a18581a1d15411d17111b052113460850104c472239564c0755015a13271e0a55553b5a47551a54010e2a06130b5506005a393013180c100f52072a4a1b5e1b165d50064e411d0521111f235f114c47362447094f10035c066f19025402191915110b4206182a544702100109133e394505175509671b6f0b01484e06505b061b50034a2911521e44431b5a233f13180b5508131523050154403740415503484f0c2602564d470a18407b775d031110004a54290319544e06505b060b424f092e1a770443101952333213030d554d551b2006064206555d50141c454f0c3d1b5e4d43061e453e39544c17580856581802001102105443101d111a043c03521455074c473f3213000a5b085d113c194f5e08555415180f5f433e270d131d420c1957773f560d11440d40543c060e470b55545b114e470e193c155f4d47110947343f13180c100f565a000403484e184c15050250081f2a54470545104c5536251325435302461a3b4a02484e12545c1b4265070b3b5440055543185b36231301025b084054220f4f42071b1554020f430b196f19564d4002055d79

去掉salt层后，就只剩下plain和key了，key就是我们要求的flag，这里我们注意到key的位数小于38位，所以使用key来循环异或加密的，对于利用重复密钥异或的情况，我们有现成的脚本Break repeating-key XOR，原理为汉明距离hamming_distance

例子

  • “karolin” and “kathrin” is 3.
  • “karolin” and “kerstin” is 3.
  • 1011101 and 1001001 is 2.
  • 2173896 and 2233796 is 3.

汉明距离（Hamming Distance） 是衡量两个字符串（或两个二进制数）之间的差异的度量。它表示的是两个字符串（或二进制数）中相同位置上不同字符的个数。简而言之，它就是计算两个字符串中对应字符不同的位置的数量。

或者

hamming_distance：在信息论中表示两个等长字符串在对应位置上不同字符的数目 以d(x, y)表示字符串x和y之间的汉明距离 简单来说 汉明距离度量了通过替换字符的方式将字符串x变成y所需要的最小的替换次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
# coding:utf-8

# python3

no_salt =bytes.fromhex('1e5d4c055104471c6f234f5501555b5a014e5d001c2a54470555064c443e235b4c0e590356542a130a4242335a47551a590a136f1d5d4d440b0956773613180b5f184015210e4f541c075a47064e5f001e2a4f711844430c473e2413011a100556153d1e4f45061441151901470a196f035b0c4443185b322e130806431d5a072a46385901555c5b550a541c1a2600564d5f054c453e32444c0a434d43182a0b1c540a55415a550a5e1b0f613a5c1f10021e56773a5a0206100852063c4a18581a1d15411d17111b052113460850104c472239564c0755015a13271e0a55553b5a47551a54010e2a06130b5506005a393013180c100f52072a4a1b5e1b165d50064e411d0521111f235f114c47362447094f10035c066f19025402191915110b4206182a544702100109133e394505175509671b6f0b01484e06505b061b50034a2911521e44431b5a233f13180b5508131523050154403740415503484f0c2602564d470a18407b775d031110004a54290319544e06505b060b424f092e1a770443101952333213030d554d551b2006064206555d50141c454f0c3d1b5e4d43061e453e39544c17580856581802001102105443101d111a043c03521455074c473f3213000a5b085d113c194f5e08555415180f5f433e270d131d420c1957773f560d11440d40543c060e470b55545b114e470e193c155f4d47110947343f13180c100f565a000403484e184c15050250081f2a54470545104c5536251325435302461a3b4a02484e12545c1b4265070b3b5440055543185b36231301025b084054220f4f42071b1554020f430b196f19564d4002055d79')
import base64
import string

def bxor(a, b):# xor two byte strings of different lengths
   if len(a) > len(b):
        return bytes([x ^ y for x, y in zip(a[:len(b)], b)])
   else:
      return bytes([x ^ y for x, y in zip(a, b[:len(a)])])
def hamming_distance(b1, b2):
    differing_bits =0

    for byte in bxor(b1, b2):
        differing_bits += bin(byte).count("1")
    return differing_bits

def score(s):
   freq = {}
   freq[' '] = 700000000
   freq['e'] = 390395169
   freq['t'] = 282039486
   freq['a'] = 248362256
   freq['o'] = 235661502
   freq['i'] = 214822972
   freq['n'] = 214319386
   freq['s'] = 196844692
   freq['h'] = 193607737
   freq['r'] = 184990759
   freq['d'] = 134044565
   freq['l'] = 125951672
   freq['u'] = 88219598
   freq['c'] = 79962026
   freq['m'] = 79502870
   freq['f'] = 72967175
   freq['w'] = 69069021
   freq['g'] = 61549736
   freq['y'] = 59010696
   freq['p'] = 55746578
   freq['b'] = 47673928
   freq['v'] = 30476191
   freq['k'] = 22969448
   freq['x'] = 5574077
   freq['j'] = 4507165
   freq['q'] = 3649838
   freq['z'] = 2456495

   score = 0
   string=bytes.decode(s)
   for c in string.lower():
       if c in freq:
            score += freq[c]
   return score

def break_single_key_xor(b1):
    max_score = 0
    english_plaintext = 0
    key = 0

    for i in range(0,256):
        b2 = [i]* len(b1)
        try:
            plaintext = bxor(b1, b2)
            pscore = score(plaintext)
        except Exception:
            continue
        if pscore > max_score or not max_score:
           max_score = pscore
           english_plaintext = plaintext
           key = chr(i)
    return key

b = no_salt

normalized_distances = []

for KEYSIZE in range(2, 40):

   # 我们取其中前6段计算平局汉明距离

   b1 = b[: KEYSIZE]
   b2 = b[KEYSIZE: KEYSIZE * 2]
   b3 = b[KEYSIZE * 2: KEYSIZE * 3]
   b4 = b[KEYSIZE * 3: KEYSIZE * 4]
   b5 = b[KEYSIZE * 4: KEYSIZE * 5]
   b6 = b[KEYSIZE * 5: KEYSIZE * 6]
   b7 = b[KEYSIZE * 6: KEYSIZE * 7]

   normalized_distance = float(
      hamming_distance(b1, b2) +
      hamming_distance(b2, b3) +
      hamming_distance(b3, b4) +
      hamming_distance(b4, b5) +
      hamming_distance(b5, b6) 
   ) / (KEYSIZE * 5)
   normalized_distances.append(
      (KEYSIZE, normalized_distance)
   )

normalized_distances = sorted(normalized_distances, key=lambda x: x[1])


for KEYSIZE, _ in normalized_distances[:5]:
   block_bytes = [[] for _ in range(KEYSIZE)]
   for i, byte in enumerate(b):
        block_bytes[i % KEYSIZE].append(byte)
   keys = ''

   for bbytes in block_bytes:
        keys += break_single_key_xor(bbytes)
   key = bytearray(keys * len(b), "utf-8")
   plaintext = bxor(b, key)
   print("keysize:", KEYSIZE)
   print("key is:", keys, "n")
   s = bytes.decode(plaintext)
   print(s)

image-20250310220753348

参考

https://www.jianshu.com/p/ecd767d9af0d

小记一类ctf密码题解题思路

https://xz.aliyun.com/t/3256#toc-22

https://cypher.codes/writing/cryptopals-challenge-set-1

https://cryptopals.com/sets/1/challenges/6

https://mp.weixin.qq.com/s?__biz=MzU3ODc2NTg1OA==&mid=2247484089&idx=1&sn=3f41f1d65595f47dc72918b22cffc128&chksm=fd7117f4ca069ee292d6bbabe37d5aa9445747d0c13dd8b2d2f1d274f7afa32f910fe28ff07e&mpshare=1&scene=23&srcid=&sharer_sharetime=1565101436270&sharer_shareid=0a12e40935fbeb4e04dfab7ff42aca93#rd

丢失的md5(暴力求解)

将代码修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import hashlib

# 迭代指定范围内的ASCII字符
for i in range(32, 127):
    for j in range(32, 127):
        for k in range(32, 127):
            # 创建要进行哈希运算的字符串
            test_string = 'TASC' + chr(i) + 'O3RJMV' + chr(j) + 'WDJKX' + chr(k) + 'ZM'
            m = hashlib.md5()
            # 将字符串编码为字节并更新哈希对象
            hashlib 模块中的 update 方法用于将数据传递给哈希对象，以便生成哈希值。在使用 update 方法时，需要传入一个字             节类型的数据。
            m.update(test_string.encode('utf-8'))
            des = m.hexdigest()
            # 检查哈希值是否包含指定的子字符串
            if 'e9032' in des and 'da' in des and '911513' in des:
                print(des)

//e9032994dabac08080091151380478a2

得到flag

Alice and Bob（质因数分离）

https://zh.numberempire.com/numberfactorizer.php

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import hashlib
def prime_factors(n):
    """
    分解给定整数n的质因数。
    返回一个列表，其中包含n的所有质因数。
    """
    # 初始化一个空列表来存储质因数
    factors = []

    # 从2开始，逐个检查每个数是否是n的因数
    for i in range(2, int(n ** 0.5) + 1):
        # 如果i是n的因数，将其添加到质因数列表中
        if n % i == 0:
            factors.append(i)
            # 如果i不是质数，则n/i也是一个因数，将其也添加到质因数列表中
            if i != n // i:
                factors.append(n // i)

                # 如果n是偶数且大于2，则它本身不是质数，需要特别处理
    if n > 2 and n % 2 == 0:
        factors.append(2)

    return factors
# 测试函数
print(prime_factors(98554799767))  # 输出: [101999, 966233]

a=hashlib.md5()
a.update("101999966233".encode('utf-8'))
print(a.hexdigest().lower())

//d450209323a847c8d01c6be47c81811a

大帝的密码武器（凯撒密码）

https://www.lddgo.net/encrypt/caesar-cipher

image-20240602144536344

下载下来的文件长这样，我们给它加上.zip后缀就能打开文件了

image-20240602144656911

从已知信息可知为凯撒密码，我们用工具进行移位

image-20240602144735700

第13位出现单词，我们把附件的字符串也移位

image-20240602144809987

得到flag{PbzrPuvan}

Windows系统密码（md5解密）

https://www.cmd5.com/

将下载的附件解压后，发现文件的后缀为hash，即原文本使用了哈希加密，众所周知，哈希密码的加密的过程被认为是不可逆的，

也就是说，人们认为从哈希串中是不可能还原出原口令的。这里我们使用记事本打开文件，得到以下内容：

image-20240602150144576

解题思路

由于哈希密码的不可逆性，我们只能借用一些工具来进行操作，这里我使用的工具网址是：MD5解密。分别对第二行的三段文字进行

求解，便可得到答案为：good-luck

信息化时代的步伐（中文电码）

image-20240602150614823

这是一串中文代码（别问我为什么知道）

找个网站解密

https://dianma.bmcx.com/

image-20240602150712490

flag出来了

凯撒？替换？呵呵!（凯撒密码爆破）

凯撒密码一般就是26个字母经过单纯的按字母顺序来位移的加密方法（一般）

如：abc=def

进阶版的凯撒就不按照字母顺序的加密

如：abc=dhj

所以就要经过暴力破解出每一种可能的对应加密

image-20240602151935377

前面的MTHJ和字符串中间的{}是明显的flag{}的格式，所以就推断这里的

MTHJ对应的明文就是flag

然后就对字符串中的其他20个字母进行爆破对比，可以写脚本（不会哈哈哈）

用工具吧

quipqiup

image-20240602151946218

flag要去空格，在两边加{}

萌萌哒的八戒（猪圈密码）

打开图片，在下面发现一些图案

image-20240602152506490

经过查询，为猪圈密码

img

对照密码表依次代入即可，得到答案为：flag{whenthepigwanttoeat}

权限获得第一步(md5解密)

image-20240602152801553

拿去md5解密就能得到flag了

传统知识+古典密码

小明某一天收到一封密信，信中写了几个不同的年份
辛卯，癸巳，丙戌，辛未，庚辰，癸酉，己卯，癸巳。
信的背面还写有“+甲子”，请解出这段密文。

key值：CTF{XXX}

img

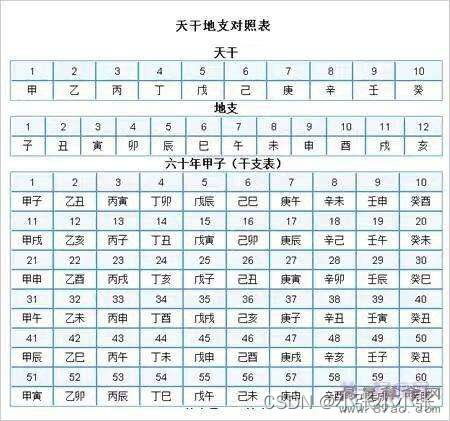
查表可得序号：28，30，23，8，17，10，16，30

且一甲子为60，所以每个加上60

88，90，83，68，77，70，76，90

对应ascii字符为

XZSDMFLZ

1
2
3
4
5
a=[88,90,83,68,77,70,76,90]
b=''
for i in a:
    b+=chr(i)
print(b)

由于古典密码只有栅栏密码和凯撒密码

我们先进行凯撒密码，移动5位进行解密得到SUNYHAGU

image-20240602155404900

再将SUNYHAGU进行栅栏密码解密

image-20240602155448691

得到flag{SHUANGYU}

世上无难事(暴力破解)

image-20240602171546125

打开页面发现一大堆字母，我们直接暴力破解

image-20240602171617317

flag记得把字母改为小写

[AFCTF2018]Morse（摩斯密码&16进制解码）

image-20240603215538129

压缩包里一看就是摩斯密码，但要把/改为空格

image-20240603215630058

解码后还需16进制解码才能得到flag

image-20240603215659800

还原大师(md5爆破).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import hashlib

mystery_md5 = "E903???4DAB????08?????51?80??8A?"
for i in range(65, 91):
    for j in range(65, 91):
        for k in range(65, 91):
            # print(f"TASC{chr(i)}O3RJMV{chr(j)}WDJKX{chr(k)}ZMd", end=";")
            # 计算候选字符串的MD5哈希值
            plaintext = f"TASC{chr(i)}O3RJMV{chr(j)}WDJKX{chr(k)}ZM"
            md5_hash = hashlib.md5(plaintext.encode('utf8')).hexdigest().upper()  # 注意大小写
            # print(md5_hash[:4])
            # 比较MD5码的部分
            if md5_hash[:4] == mystery_md5[:4]:
                print(plaintext)
                print(md5_hash)

异性相吸(二进制异或)

提起异性我们可以想到01，也就是二进制，我们用010把文件内容转化成二进制再异或

1
2
3
4
5
6
7
8
9
10
a = '0110000101110011011000010110010001110011011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011000010111001101100100011100010111011101100101011100110111000101100110'
b = '0000011100011111000000000000001100001000000001000001001001010101000000110001000001010100010110000100101101011100010110000100101001010110010100110100010001010010000000110100010000000010010110000100011000000110010101000100011100000101010101100100011101010111010001000001001001011101010010100001010000011011'
c = ''

for i in range(len(a)):
    if a[i] == b[i]:
        c += '0'
    else:
        c += '1'
print(c)

得到

1
0110011001101100011000010110011101111011011001010110000100110001011000100110001100110000001110010011100000111000001110010011100100110010001100100011011100110110011000100011011101100110001110010011010101100010001101010011010001100001001101110011010000110011001101010110010100111000001110010110010101111101

我们再解码得到flag

1
flag{ea1bc0988992276b7f95b54a7435e89e}

[GXYCTF2019]CheckIn（ROT-N加密）

image-20240611170339389

出现了两个等号，我们先base64解密

image-20240611170402562

里面没有{}可以知道不是凯撒加密，没有=不是base64

但可以发现这里的每一个字符的ASCII在33-126

可以发现是ROT-N加密

ROT-N在线加密

得到flag

image-20240611170522341

Cipher（playfair解密）

题目提示：公平的玩吧，也就是playfair，正好有这一种加密为普莱菲尔密码，以playfair为密钥进行普莱菲尔密码解密（要不是我看了wp，鬼知道这玩意）

playfair解密

image-20240611171809161

用flag{}包裹住，得到flag{itisnotaproblemhavefun}

[BJDCTF2020]这是base??（字符替换）

这题的题目是base，我们可以想到base64，但txt文档给出了2个数据，不难想到字符替代

image-20240616212448415

我们将chipertext的字符与dict的字符一一对应，得到每一个字符在dict中的下标

我们查找base64的标准字典

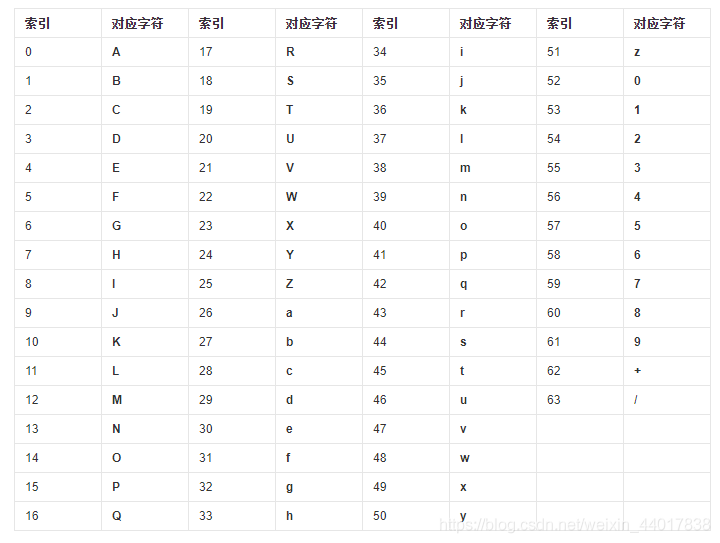
在这里插入图片描述

将每一个字符在dict中的下标与标准字典的字符相对应

写脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import base64

a={0: 'J', 1: 'K', 2: 'L', 3: 'M', 4: 'N', 5: 'O', 6: 'x', 7: 'y', 8: 'U', 9: 'V', 10: 'z', 11: 'A', 12: 'B', 13: 'C', 14: 'D', 15: 'E', 16: 'F', 17: 'G', 18: 'H', 19: '7', 20: '8', 21: '9', 22: 'P', 23: 'Q', 24: 'I', 25: 'a', 26: 'b', 27: 'c', 28: 'd', 29: 'e', 30: 'f', 31: 'g', 32: 'h', 33: 'i', 34: 'j', 35: 'k', 36: 'l', 37: 'm', 38: 'W', 39: 'X', 40: 'Y', 41: 'Z', 42: '0', 43: '1', 44: '2', 45: '3', 46: '4', 47: '5', 48: '6', 49: 'R', 50: 'S', 51: 'T', 52: 'n', 53: 'o', 54: 'p', 55: 'q', 56: 'r', 57: 's', 58: 't', 59: 'u', 60: 'v', 61: 'w', 62: '+', 63: '/', 64: '='}
b="FlZNfnF6Qol6e9w17WwQQoGYBQCgIkGTa9w3IQKw"
base64_list = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P','Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f','g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v','w', 'x', 'y', 'z', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', '/']
flag=''

for i in b:
    for j in a:
        if i == a[j]:
            flag+=base64_list[j]

print(base64.b64decode(flag))

//b'BJD{D0_Y0u_kNoW_Th1s_b4se_map}'

robomunication（音频摩斯密码）

下载文件后，发现是个音频，用Audacity打开，发现它在哔哔哔哔 哔 哔波哔哔。。。原来是摩斯密码

整理后得到：…. . .-.. .-.. — .– …. .- - .. … - …. . -.- . -.– .. - .. … -… — — .–. -… . . .–.

解码得

密码是：HELLOWHATISTHEKEYITISBOOPBEEP

最终解得flag为BOOPBEEP

[WUSTCTF2020]佛说：只能四天（解密大礼包）

image-20240818202237098

佛曰加密网站解密——http://hi.pcmoe.net/buddha.html，得到

image-20240818202346306

马上去核心价值观解密——http://www.hiencode.com/cvencode.html得到

image-20240818202511160

解密内容提示栅栏密码，我们用栅栏密码解密

要去掉后面的__doyouknowfence

栅栏密码_栅栏密码在线加密解密【W型】-ME2在线工具 (metools.info)

image-20240818204034605

我们用凯撒密码解密

image-20240818204511820

我们观察枚举后的结果都没有小写字母，我们考虑base32

在偏移为3是得到flag

img

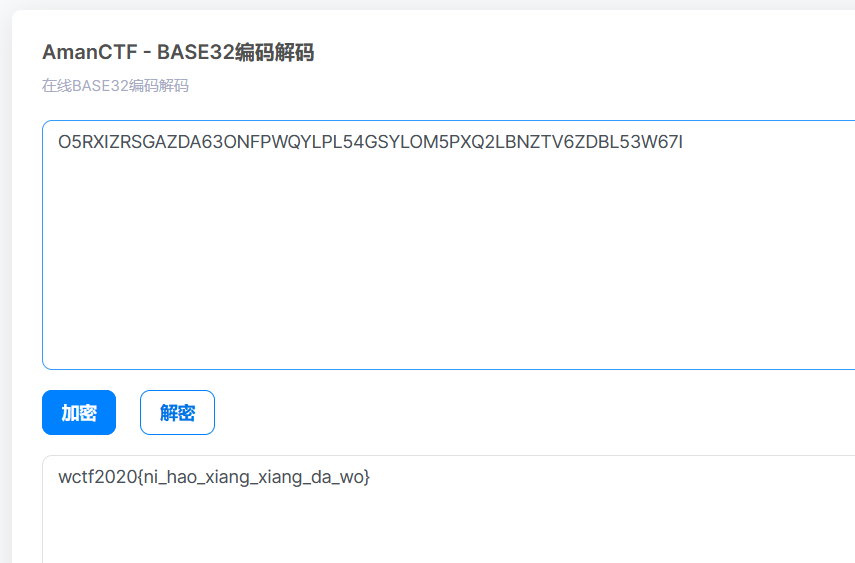
达芬奇密码（脑洞题）

image-20240818205419252

我们观察数字列发现跟斐波那契数列的数字一样但是位置不一样

我们对比来看看

1
2
3
4
5
6
7
8
def fib_loop_for(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a
for i in range(1,33):
    print(fib_loop_for(i))

1
2
3
4
5
6
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309

1 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711  

c="36968853882116725547342176952286"

我们发现数字列和神秘数字串的个数一样，所以我们猜测要通过比对斐波那契数列，来将c进行排序

例如：1在斐波那契数列中排第一位，那3就在第一位

​ 233在斐波那契数列中排第12位，那6在12位上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
a = "0 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309"
b = "0 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711"
a = a.split(" ")
b = b.split(" ")
flag = []
m = "36968853882116725547342176952286"
for i in range(len(a)):
    for j in range(len(a)):    
        if a[i] == b[j]:        #a[i]中的值在b中的索引为j
            #print(j)
            flag.append(m[j])   #将m[j]中的值添加到flag中
print(len(flag))
print(''.join(flag))
#37995588256861228614165223347687

[MRCTF2020]古典密码知多少（古典密码图形）

image-20240818205933301

观察图中信息，可以发现用到了CTF中的图形密码，包括猪圈密码的变形、标准银河字母的加密、和圣堂武士密码。

标准银河字母的加密

在这里插入图片描述

圣堂武士密码

在这里插入图片描述

解密出来得到

1
FGCPFLIRTUASYON

题目信息还提到了fence，我们考虑栅栏密码

img

可得到有用信息：FLAGISCRYPTOFUN，去掉前面信息得最终结果为：

1
flag{CRYPTOFUN}

rot(rot原理)

1
2
3
4
5
破解下面的密文：

83 89 78 84 45 86 96 45 115 121 110 116 136 132 132 132 108 128 117 118 134 110 123 111 110 127 108 112 124 122 108 118 128 108 131 114 127 134 108 116 124 124 113 108 76 76 76 76 138 23 90 81 66 71 64 69 114 65 112 64 66 63 69 61 70 114 62 66 61 62 69 67 70 63 61 110 110 112 64 68 62 70 61 112 111 112

flag格式flag{}

看着像是 ascii 码。

但是有大于 127 的数字存在，所以要先处理。

题目名称为 rot，

1
2
3
4
5
6
7
ROT5、ROT13、ROT18、ROT47 编码是一种简单的码元位置顺序替换暗码。此类编码具有可逆性，可以自我解密，主要用于应对快速浏览，或者是机器的读取，而不让其理解其意。
 
ROT5 是 rotate by 5 places 的简写，意思是旋转5个位置，其它皆同。下面分别说说它们的编码方式：
ROT5：只对数字进行编码，用当前数字往前数的第5个数字替换当前数字，例如当前为0，编码后变成5，当前为1，编码后变成6，以此类推顺序循环。
ROT13：只对字母进行编码，用当前字母往前数的第13个字母替换当前字母，例如当前为A，编码后变成N，当前为B，编码后变成O，以此类推顺序循环。
ROT18：这是一个异类，本来没有，它是将ROT5和ROT13组合在一起，为了好称呼，将其命名为ROT18。
ROT47：对数字、字母、常用符号进行编码，按照它们的ASCII值进行位置替换，用当前字符ASCII值往前数的第47位对应字符替换当前字符，例如当前为小写字母z，编码后变成大写字母K，当前为数字0，编码后变成符号_。用于ROT47编码的字符其ASCII值范围是33－126，具体可参考ASCII编码。

参考rot原理，将所有数字减13，再转ascii码

1
2
3
4
s='83 89 78 84 45 86 96 45 115 121 110 116 136 132 132 132 108 128 117 118 134 110 123 111 110 127 108 112 124 122 108 118 128 108 131 114 127 134 108 116 124 124 113 108 76 76 76 76 138 23 90 81 66 71 64 69 114 65 112 64 66 63 69 61 70 114 62 66 61 62 69 67 70 63 61 110 110 112 64 68 62 70 61 112 111 112'
l = s.split(" ")
for i in l:
    print(chr(int(i) - 13), end='')
1
2
FLAG IS flag{www_shiyanbar_com_is_very_good_????}
MD5:38e4c352809e150186920aac37190cbc

看样子我们需要对flag的最后4位进行爆破

1
2
3
4
5
6
7
8
9
10
11
12
demo='flag{www_shiyanbar_com_is_very_good_'
check = '38e4c352809e150186920aac37190cbc'
 
for i in range(32,126):
    for j in range(32,126):
        for k in range(32,126):
            for m in range(32,126):
                tmp = demo + chr(i) + chr(j) + chr(k) + chr(m) + '}'
                hash = hashlib.md5(tmp.encode('utf8')).hexdigest()
                if check == hash:
                    print(tmp)
                    exit()

得到flag

这是什么(jsfuck)

我们将apk文件修改为txt文件

我们在文件中发现

image-20240818212431110

我们考虑jsfuck解密

我们f12打开控制台，将括号复制进去

image-20240818212531846

得到flag

[MRCTF2020]天干地支+甲子（天干地支）

image-20240902205011081

1
2
3
4
5
6
7
8
9
10
11
12
13
14
六十年甲子（干支表）
1	      2	     3	      4	     5	     6	     7	     8	     9	     10
甲子	乙丑	丙寅	丁卯	戊辰	己巳	庚午	辛未	壬申	癸酉
11	     12  	 13	     14 	 15 	 16	     17	     18	     19	     20
甲戌	乙亥	丙子	丁丑	戊寅	己卯	庚辰	辛巳	壬午	癸未
21	     22    	 23	     24	     25	     26      27	     28	     29	     30
甲申	乙酉	丙戌	丁亥	戊子	己丑	庚寅	辛卯	壬辰	癸巳
31	     32	     33	     34	     35	     36	     37	     38	     39      40
甲午	乙未	丙申	丁酉	戊戌	己亥	庚子	辛丑	壬寅	癸卯
41	     42	     43	     44	     45	     46	     47	     48	     49      50
甲辰	乙巳	丙午	丁未	戊申	己酉	庚戌	辛亥	壬子	癸丑
51	     52	     53	     54	     55	     56	     57	     58	     59      60
甲寅	乙卯	丙辰	丁巳	戊午	己未	庚申	辛酉	壬戌	癸亥

我们对照得到

1
11  51  51  40  46  51  38

都加一个甲子(60)得到

1
71 111 111 100 106 111 98

我们对照ascii表得到

ASCII码表

1
2
Goodjob

得到flag

1
flag{Goodjob}

[NCTF2019]Keyboard(脑洞)

image-20240902210112608

题目提示键盘，我们发现每一个字母都对应上面的一个数字，我们猜测9键盘，而字母个数就是对应的9键盘上的对应的字母

1
2
youaresosmartthatthisisjustapieceofcake

1
2
3
4
5
6
7
8
cipher="ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee"
base=" qwertyuiop"
a=[" "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"]
for part in cipher.split(" "):
    s=base.index(part[0])
    count=len(part)
    print(a[s][count-1],end="")

[BJDCTF2020]signin

image-20240902214954471

我们观察，密文为16进制，我们将其转换为字符

1
2
3
4
from Crypto.Util.number import *
a=0x424a447b57653163306d655f74345f424a444354467d
c=long_to_bytes((a))
print(c.decode("utf-8"))

得到flag

1
BJD{We1c0me_t4_BJDCTF}

[MRCTF2020]vigenere（维吉尼亚解密）

我们找一个在线网站

https://www.guballa.de/vigenere-solver

把文本放上去，直接破解，flag是最后一行

image-20240905212644646

[ACTF新生赛2020]crypto-rsa0(zip伪加密)

我们把文件下下来后，在hint.txt提示，文件进行了zip伪加密

image-20240905215448375

一个ZIP文件由三个部分组成：

压缩源文件数据区+压缩源文件目录区+压缩源文件目录结束标志。

伪加密原理：zip伪加密是在文件头的加密标志位做修改，进而再打开文件时识被别为加密压缩包。 一般来说，文件各个区域开头就是50 4B，然后后面两个字节是版本，再后面两个就是判断是否有加密的关键了

伪加密：

压缩源文件数据区的全局加密应当为 00 00

且压缩文件目录区的全局方式标记应当为 09 00

原理

ZIP伪加密是在文件头的加密标志位做修改，进而再打开文件时识别为加密压缩包。
在参考了网上多数文章无果后，在西普的一个小题找到了可以复现的方法。
给出西普的某个示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
压缩源文件数据区 
50 4B 03 04：这是头文件标记（0x04034b50）
14 00：解压文件所需 pkware 版本 
00 00：全局方式位标记（有无加密） 
08 00：压缩方式 
5A 7E：最后修改文件时间 
F7 46：最后修改文件日期 
16 B5 80 14：CRC-32校验（1480B516）
19 00 00 00：压缩后尺寸（25）
17 00 00 00：未压缩尺寸（23）
07 00：文件名长度 
00 00：扩展记录长度 
6B65792E7478740BCECC750E71ABCE48CDC9C95728CECC2DC849AD284DAD0500  
压缩源文件目录区 
50 4B 01 02：目录中文件文件头标记(0x02014b50)  
3F 00：压缩使用的 pkware 版本 
14 00：解压文件所需 pkware 版本 
00 00：全局方式位标记（有无加密，这个更改这里进行伪加密，改为09 00打开就会提示有密码了） 
08 00：压缩方式 
5A 7E：最后修改文件时间 
F7 46：最后修改文件日期 
16 B5 80 14：CRC-32校验（1480B516）
19 00 00 00：压缩后尺寸（25）
17 00 00 00：未压缩尺寸（23）
07 00：文件名长度 
24 00：扩展字段长度 
00 00：文件注释长度 
00 00：磁盘开始号 
00 00：内部文件属性 
20 00 00 00：外部文件属性 
00 00 00 00：局部头部偏移量 
6B65792E7478740A00200000000000010018006558F04A1CC5D001BDEBDD3B1CC5D001BDEBDD3B1CC5D001  
压缩源文件目录结束标志 
50 4B 05 06：目录结束标记 
00 00：当前磁盘编号 
00 00：目录区开始磁盘编号 
01 00：本磁盘上纪录总数 
01 00：目录区中纪录总数 
59 00 00 00：目录区尺寸大小 
3E 00 00 00：目录区对第一张磁盘的偏移量 
00 00：ZIP 文件注释长度
		我们用010打开zip文件，把所有的50 4B后的09 00都改成00 00

image-20240905215619133

保存之后打开压缩包，发发现就可以顺利打开rsa.py文件了

然后就是个rsa解密了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import binascii
import gmpy2
import binascii

p = 9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
q = 7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
c = 50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350
e = 65537

n = p * q
phi_n = (q - 1) * (p - 1)
d = gmpy2.invert(e, phi_n)
m = gmpy2.powmod(c, d, n)

print(binascii.unhexlify(hex(m)[10:]))

传感器（曼彻斯特编码）

Wiki

曼彻斯特编码（Manchester Encoding），也叫做相位编码（ Phase Encode，简写PE），是一个同步时钟编码技术，被物理层使用来编码一个同步位流的时钟和数据。它在以太网媒介系统中的应用属于数据通信中的两种位同步方法里的自同步法（另一种是外同步法），即接收方利用包含有同步信号的特殊编码从信号自身提取同步信号来锁定自己的时钟脉冲频率，达到同步目的。

Encode and Decode

IEEE 802.4（令牌总线）和低速版的IEEE 802.3（以太网）中规定, 按照这样的说法, 01电平跳变表示1, 10的电平跳变表示0。

Ideas
1
2
3
4
5
6
7
8
9
5555555595555A65556AA696AA6666666955`转为二进制，根据01->1,10->0。可得到
0101->11
0110->10
1010->00
1001->01
decode得到
`11111111 11111111 01111111 11001011 11111000 00100110 00001010 10101010 10011111`
bin->hex，对比ID并不重合，根据八位倒序传输协议将二进制每八位reverse，转hex即可
flag：`FFFFFED31F645055F9
1
2
3
4
5
6
7
8
9
10
11
cipher='5555555595555A65556AA696AA6666666955'
def iee(cipher):
    tmp=''
    for i in range(len(cipher)):
        a=bin(eval('0x'+cipher[i]))[2:].zfill(4)
        tmp=tmp+a[1]+a[3]
        print(tmp)
    plain=[hex(int(tmp[i:i+8][::-1],2))[2:] for i in range(0,len(tmp),8)]
    print(''.join(plain).upper())

iee(cipher)

[NPUCTF2020]这是什么觅🐎（观察）

用记事本打开是个乱码·

image-20240909151824355

但我们看到开头那个pk，我们想到zip文件，我们将后缀改为zip，成功打开文件

image-20240909151910551

看到有一个字条和日历，猜测是类似矩阵的原理,

1
F1 W1 S22 S21 T12 S11 W1 S13

两个s应该是s1对应周六，s2对应周日

字母最后的数字对应所在的行数

例如F1，第一行的星期五

1
3 1 12 5 14 4 1 18

对照字母表 calendar，flag{calendar}

浪里淘沙（脑洞）

打开txt文档发现大量的单词，再结合题目给到的一串数字4、8、11、15、16可以考虑到是跟字频有关

我们打开万能的wps进行查询

image-20240914150507182

然后放到excel进行排序

image-20240914150532083

标注起题目要求的编号组合起字符串即可得到flag

flag{weshouldlearnthecrypto}

[WUSTCTF2020]B@se（base64变表&排列组合）

题目附件内容：

image-20241022191416972

首先通过观察题目字符特征很明显是base64编码，第一行的密文是通过下面给的base64的变表，但是仔细观察缺少了四个字符，因此我们需要写脚本把缺少的字符给还原出来

爆破脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import string
c = 'JASGBWcQPRXEFLbCDIlmnHUVKTYZdMovwipatNOefghq56rs****kxyz012789+/'
for i in string.ascii_letters + string.digits:  # string.ascii_letters所有字母  string.digits所有数字
    if(i not in c):
        print(i,end='')
# ju34

很明显爆破出来的是“ju34”，但是我们还不知道他的原始排列的顺序是什么？，因此需要我们对着四个字符与密文进行一个排列组合，并可以解出明文。
代码如下（这里是参考了一些大佬的脚本）：
import binascii
import itertools
cipher = 'MyLkTaP3FaA7KOWjTmKkVjWjVzKjdeNvTnAjoH9iZOIvTeHbvD' # 全排列组合
s = ['j','u','3','4']
for i in itertools.permutations(s,4): # 4就是把s列表里的字母4个为一组排列
    k = "JASGBWcQPRXEFLbCDIlmnHUVKTYZdMovwipatNOefghq56rs"+ "".join(i) + "kxyz012789+/"  # "".join(i)排列的结果（join() 方法用于将序列中的元素以指定的字符连接生成一个新的字符串）
    a = ""
    for j in cipher:
        a += bin(k.index(j))[2:].zfill(6)
    print(binascii.a2b_hex(hex(eval("0b"+a))[2:-1]))  # a2b_hex和binascii.unhexlify可以为16进制的 bytes 类型，也可以为十六进制 str 类型
                                                      # 举例：这里转为16进制后会出现0x471L，所以只有去掉0x和L就有了[2:-1]

运行结果：

img

很明显图中框出来的地方就是最后的flag值

总结：此题考察了缺损的base64变表，需要使用爆破脚本破解出明文。

[AFCTF2018]Single（爆破）

我们下载附件，发现里面有个c语言程序和一个文件

通过代码分析，我们发现Cipher.txt是一个加密后的文件，仔细观察，很明显示是一个无规律替换加密，我们使用词频分析

网站：http://quipqiup.com/

得到flag

image-20240926192619737

或者我们逆向输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;
int main()
{
	freopen("Cipher.txt","r",stdin);//输入输出换一下
	freopen("Plain.txt","w",stdout);//输入输出换一下
	map<char, char> f;
	int arr[26];
	for(int i=0;i<26;++i){
		arr[i]=i;
	}
	random_shuffle(arr,arr+26);
	for(int i=0;i<26;++i){
		f['a'+i]='a'+arr[i];
		f['A'+i]='A'+arr[i];
	}
	char ch;
	while((ch=getchar())!=EOF){
		if(f.count(ch)){
            //反向转换一下，通过value>>key
			for(map<char,char>::iterator it = f.begin();it!=f.end();it++)
			{
				if(it->second == ch)
				{
				  putchar(it->first);
				  break;
				}
			}
		}else{
			putchar(ch);
		}
	}
	return 0;
}

得到加密前的文件，找到flag

鸡藕椒盐味（海明校验码）

image-20241009211038399

1.分析校验位数

从题目可知验证码为110010100000共12位，校验位一般都是在2^n的位置，所以共有4位校验码在1，2，4，8位置

拓展：海明验证码公式：2^r≥k+r+1 （r为校验位 ，k为信息位），如本验证码本来有8位信息码，带入公式可得r=4，所以在1，2，4，8位置添加相应校验码

2.画表

题目中提到打印的时候倒了一下，所以将信息位倒着填入表中

1 2 3 4 5 6 7 8 9 10 11 12 位数
0 0 1 0 0 0 1 1 信息位（D）
R1 R2 R3 R4 校验位（R）

3.求校验位的值

例如：1由第一位R1来校验；2由第二位R2来校验；由于3=1+2（1和2指的是位数，都是2的n次方）所以3由第一位R1和第二位R2校验，4由第四位R3校验，5和3道理是一样的，5=1+4（2^0+2^2）;6=2+4;7=1+2+4，依次类推。得出下表：

海明码位号 占用的校验位号 校验位
1 1 R1
2 2 R2
3 1、2 R1、R2
4 4 R3
5 1、4 R1、R3
6 2、4 R2、R3
7 1、2、4 R1、R2、R3
8 8 R4
9 1、8 R1、R4
10 2、8 R2、R4
11 1、2、8 R1、R2、R4
12 4、8 R3、R4

进行汇总，看每个校验位都确定了哪一位。

R1：1、3、5、7、9、11

R2：2、3、6、7、10、11

R3：4、5、6、7、12

R4：9、10、11、12

最后用异或运算求出R1、R2、R3、R4、R5的值（以R1为例）：

R1=D1⊕D3⊕D5⊕D7⊕D9⊕D11=1

以此类推：R1=1,R2=0,R3=0,R4=0

可以看到P1P2P3P4=0001,R1R2R3R4=1000

可以求得监督位（异或）：

0 0 0 1 验证码中的校验码
1 0 0 0 求得的校验码
1 0 0 1 监督位

监督位不为0000，说明接收方生成的校验位和收到的校验位不同，错误的位数是监督位的十进制即9，所以把D9就是题目中提到的错误，得到正确验证码110110100000，然后根据提示MD5hash一下就出来了。

1
2
3
4
5
6
7
8
1 import hashlib
2 c="110110100000"
3 md=hashlib.md5()
4 md.update(c.encode("utf8"))
5 flag = md.hexdigest()
6 print(flag)
7 
8 #d14084c7ceca6359eaac6df3c234dd3b

套入flag{}即可得到答案flag{d14084c7ceca6359eaac6df3c234dd3b}

[AFCTF2018]BASE(base16,32,64解密)

我们随便截取文件的一段内容，发现能进行多段base64解密

我们找个脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import re
import base64
s=open('flag_encode.txt','rb').read()
base16_dic = r'^[A-F0-9=]*$'
base32_dic = r'^[A-Z2-7=]*$'
base64_dic = r'^[A-Za-z0-9/+=]*$'
n= 0
while True:
    n += 1
    t = s.decode()
    if '{' in t:
        print(t)
        break
    elif re.match(base16_dic, t):
        s = base64.b16decode(s)
        print(str(n) + ' base16')
    elif re.match(base32_dic, t):
        s = base64.b32decode(s)
        print(str(n) + ' base32')
    elif re.match(base64_dic, t):
        s = base64.b64decode(s)
        print(str(n) + ' base64')

[BJDCTF2020]Polybius(波利比奥斯方阵密码)

由题目我们知道这个题目的考点是波利比奥斯方阵

Polybius校验表如下

image-20241106212727853

(2,4)这个坐标既可以表示i 也可以表示 j因此破解的时候这里又会多两种情况

我们来康个例子

假设明文序列为attack at once，使用一套秘密混杂的字母表填满波利比奥斯方阵

如下

image-20241106213011152

  1. i 和 j视为同一格
  2. 选择这五个字母，是因为它们译成摩斯密码时不容易混淆，可以降低传输错误的机率

根据上面的Polybius方阵将对应的明文进行加密。其中，A,D,F,G,X也可以用数字1,2,3,4,5来代替，这样密文就成了：

明文 A T T A C K A T O N C E
密文 AF AD AD AF GF DX AF AD DF FX GF XF
13 12 12 13 43 25 13 12 23 35 43 53

我们来分析题目

密文：ouauuuoooeeaaiaeauieuooeeiea

hint: VGhlIGxlbmd0aCBvZiB0aGlzIHBsYWludGV4dDogMTQ=

基本的解题方阵如下

image-20241106213917475

base64解密后信息为The length of this plaintext: 14，提示长度为14，但是a,e,o,i,u这五个字符的代表顺序却不知道,因此可能有54321种情况,在结合刚才所说的i,j同时占一个位置,所以情况数要再乘上2,将这些情况全部都打印出来,然后去找有真实语义的句子就可以了.所以密文为14×2位，可以推测为波利比奥斯方阵密码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import itertools
ciper = 'ouauuuoooeeaaiaeauieuooeeiea'
head = 'aeoiu'
headlist = []
num_headlist = []

# 先列举处aeiou五种的不同排序
x = itertools.permutations(head,5)
for i in x:
    temp = "".join(i)
    headlist.append(temp)
print(headlist)

# 根据aeiou对应的12345修改ciper的对应值，便于后续的遍历得到结果
for i in headlist:
    temp = ''
    for j in ciper:
        temp += str(i.index(j) + 1)        
    num_headlist.append(temp)
print(num_headlist)

# 将ciper对应的数字乘上比例加上96再转为ASCII码，即 可得到对应的字母
for i in num_headlist:
    temp = ''
    for j in range(0,len(i),2):
        xx = (int(i[j]) - 1)*5 + int(i[j+1]) + 96   # 前一个为乘上5加上后一个就正好对应了表格中的字母
        if xx>ord('i'):
            xx+=1
        temp += chr(xx)
    print(temp)

https://www.cnblogs.com/labster/p/13842837.html

四面八方（四方密码）

根据题目提示，该题考的是四方密码

四方密码用4个5×5的矩阵来加密。每个矩阵都有25个字母（通常会取消Q或将I,J视作同一样，或改进为6×6的矩阵，加入10个数字）。

加密原理：

首先选择两个英文字作密匙，例如example和keyword。对于每一个密匙，将重复出现的字母去除，即example要转成exampl，然后将每个字母顺序放入矩阵，再将余下的字母顺序放入矩阵，便得出加密矩阵。

将这两个加密矩阵放在右上角和左下角，余下的两个角放a到z顺序的矩阵： [1]

加密的步骤：

两个字母一组地分开讯息：（例如hello world变成he ll ow or ld）；

找出第一个字母在左上角矩阵的位置；

同样道理，找第二个字母在右下角矩阵的位置；

找右上角矩阵中，和第一个字母同行，第二个字母同列的字母；

找左下角矩阵中，和第一个字母同列，第二个字母同行的字母；

得到的这两个字母就是加密过的讯息。

he lp me ob iw an ke no bi的加密结果：FY NF NE HW BX AF FO KH MD

引用大佬博客中的一张图片：

在这里插入图片描述

再回到本题

由key1:security和 key2:information可以确认阵图

abcde SECUR

fghij ITYAB

klmno DFGHJ

prstu KLMNO

vwxyz PVWXZ

INFOR abcde

MATBC fghij

DEGHJ klmno

KLPSU prstu

VWXYZ vwxyz

要解密的密文为zh nj in ho op cf cu kt lj

按照刚才的方法解密为：yo un ga nd su cc es sf ul

flag{youngandsuccessful}

也可以用脚本

我们引用大佬脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
import collections
import re
 
matrix = 'ABCDEFGHIJKLMNOPRSTUVWXYZ'
pla = 'abcdefghijklmnoprstuvwxyz'
key1 = '[SECURITY]'
key2 = '[INFORMATION]'
key1 = ''.join(collections.OrderedDict.fromkeys(key1))
key2 = ''.join(collections.OrderedDict.fromkeys(key2))
 
matrix1 = re.sub('[\[\]]','',key1) + re.sub(key1,'',matrix)
matrix2 = re.sub('[\[\]]','',key2) + re.sub(key2,'',matrix)
 
matrix_list1 = []
matrix_list2 = []
pla_list = []
for i in range(0,len(matrix1),5):
matrix_list1.append(list(matrix1[i:i+5]))
#print matrix_list1
 
for i in range(0,len(matrix2),5):
matrix_list2.append(list(matrix2[i:i+5]))
#print matrix_list2
 
for i in range(0,len(pla),5):
pla_list.append(list(pla[i:i+5]))
#print pla_list
 
#查询两个密文字母位置
def find_index1(x):
for i in range(len(matrix_list1)):
for j in range(len(matrix_list1[i])):
if matrix_list1[i][j] == x:
return i,j
def find_index2(y):
for k in range(len(matrix_list2)):
for l in range(len(matrix_list2[k])):
if matrix_list2[k][l] == y:
return k,l
 
def gen_pla(letter):
 
#两个子母中第一个字母位置
first = find_index1(letter[0])
 
#两个子母中第二个字母位置
second = find_index2(letter[1])
 
pla = ''
pla += pla_list[first[0]][second[1]]
pla += pla_list[second[0]][first[1]]
 
return pla
 
def main():
cip = 'ZHNJINHOOPCFCUKTLJ'
pla = ''
for i in range(0,len(cip),2):
pla += gen_pla(cip[i:i+2])
print (pla)
 
if __name__ == '__main__':
main()import collections
import re

matrix = 'ABCDEFGHIJKLMNOPRSTUVWXYZ'
pla = 'abcdefghijklmnoprstuvwxyz'
key1 = '[SECURITY]'
key2 = '[INFORMATION]'
key1 = ''.join(collections.OrderedDict.fromkeys(key1))
key2 = ''.join(collections.OrderedDict.fromkeys(key2))

matrix1 = re.sub('[\[\]]', '', key1) + re.sub(key1, '', matrix)
matrix2 = re.sub('[\[\]]', '', key2) + re.sub(key2, '', matrix)

matrix_list1 = []
matrix_list2 = []
pla_list = []
for i in range(0, len(matrix1), 5):
    matrix_list1.append(list(matrix1[i:i + 5]))
# print matrix_list1

for i in range(0, len(matrix2), 5):
    matrix_list2.append(list(matrix2[i:i + 5]))
# print matrix_list2

for i in range(0, len(pla), 5):
    pla_list.append(list(pla[i:i + 5]))


# print pla_list

# 查询两个密文字母位置
def find_index1(x):
    for i in range(len(matrix_list1)):
        for j in range(len(matrix_list1[i])):
            if matrix_list1[i][j] == x:
                return i, j


def find_index2(y):
    for k in range(len(matrix_list2)):
        for l in range(len(matrix_list2[k])):
            if matrix_list2[k][l] == y:
                return k, l


def gen_pla(letter):


# 两个子母中第一个字母位置
    first = find_index1(letter[0])

    # 两个子母中第二个字母位置
    second = find_index2(letter[1])

    pla = ''
    pla += pla_list[first[0]][second[1]]
    pla += pla_list[second[0]][first[1]]

    return pla


def main():
    cip = 'ZHNJINHOOPCFCUKTLJ' //密文


    pla = ''
    for i in range(0, len(cip), 2):
        pla += gen_pla(cip[i:i + 2])
    print(pla)

if __name__ == '__main__':
    main()

[ACTF新生赛2020]crypto-classic1(键盘包围密码&维吉尼亚)

首先是个26键键盘包围密码解密，得到压缩包密码circle

解压，得到维吉尼亚密码

1
SRLU{LZPL_S_UASHKXUPD_NXYTFTJT}

再利用脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# coding=utf-8

# 通过前4个字母，计算出key:
s1 = 'SRLU'
s2 = 'ACTF'
key = ''
for i in range(4):
    key += chr((ord(s1[i])-ord(s2[i]))%26 + ord('A'))
print(key)
l = len(key)
print(l)
# key='SPSP'
# 4

c = 'SRLU{LZPL_S_UASHKXUPD_NXYTFTJT}'
m = []
l_c = len(c)
for i in range(l_c):
    if 'A'<=c[i]<='Z':
        if ord(c[i]) < ord(key[i % l]):
            m.append(chr(ord(c[i]) - ord(key[i % l]) + ord('A') + 26))
        else:
            m.append(chr(ord(c[i]) - ord(key[i % l]) + ord('A')))
    else:
        m.append(c[i])
print(m)

l = len(m)
flag = ''
for i in range(l):
    flag += m[i]
print(flag.lower())

EasyProgram（伪代码）

image-20241119215705588

看了下，没看懂啥语言，应该是伪代码吧，这道题的flag的加密其实就一句话

1
set flag[m]:flag[m]^s[x]

要逆向很简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#读文件方法一：
def filehex(file):
    fhex=[]
    f = open(file,'rb')
    ff = f.read().hex()
 
    for i in range(0,len(str(ff)),2):
        fhex.append(int(str(ff)[i:i+2],16))
    return fhex
 
flagx2=filehex('file.txt')
print(flagx2)
 
#读文件方法二：使用010edit 读取'file.txt'文件16进制
flagx=[0x00,0xBA,0x8F,0x11,0x2B,0x22,0x9F,0x51,0xA1,0x2F,0xAB,0xB7,0x4B,0xD7,0x3F,0xEF,0xE1,0xB5,0x13,0xBE,0xC4,0xD4,0x5D,0x03,0xD9,0x00,0x7A,0xCA,0x1D,0x51,0xA4,0x73,0xB5,0xEF,0x3D,0x9B,0x31,0xB3]
 
s=[]
t=[]
key='whoami'
j=0
for i in range(0,256):
    s.append(i)
 
for i in range(0,256):
    t.append(key[i % len(key)])
 
for i in range(0,256):
     j=(j+int(s[i])+int(ord(t[i])))%256
     s[i], s[j] = s[j], s[i]
 
i=0;j=0;x=0
for m in range(0,38):
    i=(i + 1)%(256)
    j=(j + s[i])%(256)
    s[i],s[j] = s[j],s[i]
    x=(s[i] + (s[j]%(256)))%(256)
    flagx[m] = flagx[m] ^ s[x]
    flagx2[m]=flagx2[m]^s[x]
 
print(''.join(chr(flagx[i]) for i in range(0,38)))
print(''.join(chr(flagx2[i]) for i in range(0,38)))

[GUET-CTF2019]NO SOS(凯撒密码，培根密码)

一眼看去是摩斯密码，但有点错误

我们先修正，得到

1
..-.-.-.--.......--..-...-..-...--.-.-....-..-..--.-.-..-.-..----

解码后得到

1
aababababbaaaaaaabbaabaaabaabaaabbababaaaabaabaabbababaababaabbbb

看到字符串里只含有ab，我们想到培根密码

在这里插入图片描述

解密得到flag

image-20241202210024381

[UTCTF2020]hill(希尔密码)

希尔密码

每个字母当作26进制数字：A=0, B=1, C=2… 一串字母当成n维向量，跟一个n×n的矩阵相乘，再将得出的结果模26。

注意用作加密的矩阵（即密匙）在

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-35afbMB0-1627306365129)(https://bkimg.cdn.bcebos.com/formula/1af1cfeb705030c3fd09342022a87f9d.svg)]

必须是可逆的，否则就不可能解码。只有矩阵的行列式和26互质，才是可逆的。

这题就是个二阶希尔密码加密。知道密文前6位wznqca和明文前6位utflag，等于4个未知数6个一阶方程，居然还有解，那就是二阶跑不了了。

然后根据 wznqca = utflag 解出ABCD (是mod26意义下的！)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from string import *
s = "duqopfkqnwofdbzgeu"

def Find(a1,a2,a3,a4,a5,a6,b1,b2,b3,b4,b5,b6):
    for c1 in range(26):
        for c2 in range(26):
            for c3 in range(26):
                for c4 in range(26):
                    if(((c1*a1+c2*a4)%26 == b1) and ((c1*a2+c2*a5)%26 == b2) and ((c1*a3+c2*a6)%26 == b3) \
                    and((c3*a1+c4*a4)%26 == b4) and ((c3*a2+c4*a5)%26 == b5) and ((c3*a3+c3*a6)%26 == b6)):
                        return (c1,c2,c3,c4)

c = Find(22,13,2,25,16,0,20,5,0,19,11,6)
A,C,B,D = c[0],c[1],c[2],c[3]
flag = ""
for i in range(0,len(s),2):
    flag += ascii_letters[(A*ascii_letters.index(s[i])+C*ascii_letters.index(s[i+1]))%26]
    flag += ascii_letters[(B*ascii_letters.index(s[i])+D*ascii_letters.index(s[i+1]))%26]

print(flag)
# d4nger0us_c1pherText_qq
# d4uqop0fk_q1nwofDbzg_eu


[AFCTF2018]你听过一次一密么？(一次一密加密)

转载https://www.ruanx.net/many-time-pad/

buu附件有问题，应该为

1
2
3
4
5
6
7
8
9
10
11
25030206463d3d393131555f7f1d061d4052111a19544e2e5d54
0f020606150f203f307f5c0a7f24070747130e16545000035d54
1203075429152a7020365c167f390f1013170b1006481e13144e
0f4610170e1e2235787f7853372c0f065752111b15454e0e0901
081543000e1e6f3f3a3348533a270d064a02111a1b5f4e0a1855
0909075412132e247436425332281a1c561f04071d520f0b1158
4116111b101e2170203011113a69001b47520601155205021901
041006064612297020375453342c17545a01451811411a470e44
021311114a5b0335207f7c167f22001b44520c15544801125d40
06140611460c26243c7f5c167f3d015446010053005907145d44
0f05110d160f263f3a7f4210372c03111313090415481d49530f

　本文讨论的加密方式是最简单的一种：简单异或。准备一个 key 字符串，然后利用 key 去异或相同长度的明文，即得到密文。如果每个密文都利用新的 key 去加密，那么这种方式称为“一次一密”（One-Time-Pad）。OTP是无条件安全的：即使攻击者拥有无限的计算资源，都不可能破译OTP加密的密文。

　　然而，一次一密的密钥分发是比较困难的。首先，Alice 想要 给 Bob 发送长度为 n 的信息，则必须在这之前传送长度为 n 的密钥，相当于传输的数据总量翻了倍。其次，尽管密文是无条件安全的，但密钥的传输信道未必是安全的，攻击者一旦窃听了密钥，则可以解密密文。

　　那么马上就可以想到一个投机取巧的方法—— Alice 造一个比较长的密钥，然后用非常秘密的方式告诉 Bob. 接下来，Alice 每次向 Bob 发送信息，都把明文异或上这个约定好的字符串；Bob 收到信息之后，把密文异或上 key, 于是就可以拿到明文。整个过程只需要传送一次密钥，这是很方便的。这种方式称为 Many-Time-Pad (MTP).

　　很遗憾，上述的 MTP 办法是不安全的。攻击者如果截获了足够多的密文，就有可能推断出明文、进而拿到密钥。这个缺陷是异或运算的性质带来的。

　上述的每一个字符串 Ci，都是某个 key 异或上明文 Mi 得到的。我们的目标是获取这个 key. 已知明文是英文句子。

　　回顾异或运算的性质：结合律、交换律、逆元为其自身。这是非常好的性质，然而也为攻击者提供了方便。因为：

C1⊕C2=(M1⊕key)⊕(M2⊕key)=M1⊕M2

　　这表明，两个密文的异或，就等于对应明文的异或。这是很危险的性质，高明的攻击者可以通过频率分析，来破译这些密文。我们来看字符串 C1 异或上其他密文会得到什么东西。以下只保留了英文字符，其余字符以 “.” 代替。

这表明，两个密文的异或，就等于对应明文的异或。这是很危险的性质，高明的攻击者可以通过频率分析，来破译这些密文。我们来看字符串 C1 异或上其他密文会得到什么东西。以下只保留了英文字符，其余字符以 “.” 代替。

1
2
3
4
5
6
7
8
9
10
....S....N.U.....A..M.N...
...Ro..I...I....SE....P.I.
.E..H...IN..H...........TU
..A.H.R.....E....P......E.
...RT...E...M....M....A.L.
d...V..I..DNEt........K.DU
.......I....K..I.ST...TiS.
.....f...N.I........M.O...
.........N.I...I.S.I..I...
....P....N.OH...SA....Sg..

　　可以观察到，有些列上有大量的英文字符，有些列一个英文字符都没有。这是偶然现象吗？

ascii表

　　ascii 码表在 Linux 下可以通过 man ascii 指令查看。它的性质有：

  • 0x20 是空格。 低于 0x20 的，全部是起特殊用途的字符； 0x20~0x7E 的，是可打印字符。
  • 0x30~0x39 是数字 0,1,2...9。
  • 0x41~0x5A 是大写字母 A-Z； 0x61~0x7A 是小写字母 a-z.

　　我们可以注意到一个至关重要的规律：小写字母 xor 空格，会得到对应的大写字母；大写字母 xor 空格，会得到小写字母！所以，如果 x⊕y 得到一个英文字母，那么 x,y 中的某一个有很大概率是空格。再来回头看上面 C1 xor 其他密文——也就等于 M1 xor 其他明文的表，如果第 col 列存在大量的英文字母，我们可以猜测 M1[col] 是一个空格。那一列英文字母越多，把握越大。

　　知道 M1 的 col 位是空格有什么用呢？别忘了异或运算下，x 的逆元是其自身。所以Mi[col]=M1[col]⊕Mi[col]⊕M1[col]=M1[col]⊕Mi[col]⊕0x20

　　于是，只要知道某个字符串的某一位是空格，我们就可以恢复出所有明文在这一列的值。

攻击

　　攻击过程显而易见：对于每一条密文Ci，拿去异或其他所有密文。然后去数每一列有多少个英文字符，作为“Mi在这一位是空格”的评分。

　　上面的事情做完时候，依据评分从大到小排序，依次利用 “某个明文的某一位是空格” 这种信息恢复出所有明文的那一列。如果产生冲突，则舍弃掉评分小的。不难写出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False

def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

c = [codecs.decode(x.strip().encode(), 'hex') for x in open('Problem.txt', 'r').readlines()]

msg = np.zeros([len(c), len(c[0])], dtype=int)

getSpace()

dat = sorted(dat)[::-1]
for w, index, pos in dat:
    infer(index, pos)

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

　　执行代码，得到的结果是：

1
2
3
4
5
6
7
8
9
10
11
Dear Friend, T%is tim< I u
nderstood my m$stake 8nd u
sed One time p,d encr ptio
n scheme, I he,rd tha- it 
is the only en.ryptio7 met
hod that is ma9hemati:ally
 proven to be #ot cra:ked 
ever if the ke4 is ke)t se
cure, Let Me k#ow if  ou a
gree with me t" use t1is e
ncryption sche e alwa s...

　　显然这不是最终结果，我们得修正几项。把 “k#now” 修复成 “know”，把 “alwa s” 修复成 “always”. 代码如下：

1
2
3
4
5
6
7
8
9
10
def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)

know(10, 21, 'y')
know(8, 14, 'n')

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

　　结果得到：

1
2
3
4
5
6
7
8
9
10
11
Dear Friend, This time I u
nderstood my mistake and u
sed One time pad encryptio
n scheme, I heard that it 
is the only encryption met
hod that is mathematically
 proven to be not cracked 
ever if the key is kept se
cure, Let Me know if you a
gree with me to use this e
ncryption scheme always...

　　我们成功恢复了明文！那么 key 也很好取得了：把 C1 异或上 M1 即可。

1
2
3
4
key = xo.strxor(c[0], ''.join([chr(c) for c in msg[0]]).encode())
print(key)

# b'afctf{OPT_1s_Int3rest1ng}!'

结论

　　Many-Time-Pad 是不安全的。我们这一次的攻击，条件稍微有点苛刻：明文必须是英文句子、截获到的密文必须足够多。但是只要攻击者有足够的耐心进行词频分析、监听大量密文，还是能够发起极具威胁性的攻击。如果铁了心要用直接xor来加密信息，应当采用一次一密(One-Time-Pad).

　　完整的解题脚本如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False


def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)


dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

c = [codecs.decode(x.strip().encode(), 'hex') for x in open('Problem.txt', 'r').readlines()]

msg = np.zeros([len(c), len(c[0])], dtype=int)

getSpace()

dat = sorted(dat)[::-1]
for w, index, pos in dat:
    infer(index, pos)

know(10, 21, 'y')
know(8, 14, 'n')

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

key = xo.strxor(c[0], ''.join([chr(c) for c in msg[0]]).encode())
print(key)

[BJDCTF2020]伏羲六十四卦

1
2
3
4
5
6
这是什么，怎么看起来像是再算64卦！！！

密文:升随临损巽睽颐萃小过讼艮颐小过震蛊屯未济中孚艮困恒晋升损蛊萃蛊未济巽解艮贲未济观豫损蛊晋噬嗑晋旅解大畜困未济随蒙升解睽未济井困未济旅萃未济震蒙未济师涣归妹大有
嗯？为什么还有个b呢?
b=7
flag：请按照格式BJD{}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# -- coding:UTF-8 --
from secret import flag

def encrpyt5():
    enc=''
    for i in flag:
        enc+=chr((a*(ord(i)-97)+b)%26+97)
    return(enc)

def encrypt4():
    temp=''
    offset=5
    for i in range(len(enc)):
        temp+=chr(ord(enc[i])-offset-i)
    return(temp)

脑洞挺逆天的题

我们需要将密文中出现的卦象按照顺序转化为6位的二进制数，然后再利用字典将密文转化为二进制字符串

字典（不清楚咋排的）

1
dic={'坤': '000000', '剥': '000001', '比': '000010', '观': '000011', '豫': '000100', '晋': '000101', '萃': '000110', '否': '000111', '谦': '001000', '艮': '001001', '蹇': '001010', '渐': '001011', '小过': '001100', '旅': '001101', '咸': '001110', '遁': '001111', '师': '010000', '蒙': '010001', '坎': '010010', '涣': '010011', '解': '010100', '未济': '010101', '困': '010110', '讼': '010111', '升': '011000', '蛊': '011001', '井': '011010', '巽': '011011', '恒': '011100', '鼎': '011101', '大过': '011110', '姤': '011111', '复': '100000', '颐': '100001', '屯': '100010', '益': '100011', '震': '100100', '噬嗑': '100101', '随': '100110', '无妄': '100111', '明夷': '101000', '贲': '101001', '既济': '101010', '家人': '101011', '丰': '101100', '离': '101101', '革': '101110', '同人': '101111', '临': '110000', '损': '110001', '节': '110010', '中孚': '110011', '归妹': '110100', '睽': '110101', '兑': '110110', '履': '110111', '泰': '111000', '大畜': '111001', '需': '111010', '小畜': '111011', '大壮': '111100', '大有': '111101', '夬': '111110', '乾': '111111'}

然后根据字典将密文转化为二进制字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
a = '升随临损巽睽颐萃小过讼艮颐小过震蛊屯未济中孚艮困恒晋升损蛊萃蛊未济巽解艮贲未济观豫损蛊晋噬嗑晋旅解大畜困未济随蒙升解睽未济井困未济旅萃未济震蒙未济师涣归妹大有'
dic={'坤': '000000', '剥': '000001', '比': '000010', '观': '000011', '豫': '000100', '晋': '000101', '萃': '000110', '否': '000111', '谦': '001000', '艮': '001001', '蹇': '001010', '渐': '001011', '小过': '001100', '旅': '001101', '咸': '001110', '遁': '001111', '师': '010000', '蒙': '010001', '坎': '010010', '涣': '010011', '解': '010100', '未济': '010101', '困': '010110', '讼': '010111', '升': '011000', '蛊': '011001', '井': '011010', '巽': '011011', '恒': '011100', '鼎': '011101', '大过': '011110', '姤': '011111', '复': '100000', '颐': '100001', '屯': '100010', '益': '100011', '震': '100100', '噬嗑': '100101', '随': '100110', '无妄': '100111', '明夷': '101000', '贲': '101001', '既济': '101010', '家人': '101011', '丰': '101100', '离': '101101', '革': '101110', '同人': '101111', '临': '110000', '损': '110001', '节': '110010', '中孚': '110011', '归妹': '110100', '睽': '110101', '兑': '110110', '履': '110111', '泰': '111000', '大畜': '111001', '需': '111010', '小畜': '111011', '大壮': '111100', '大有': '111101', '夬': '111110', '乾': '111111'}
s = ''
i = 0
while i < len(a):
    try:
        s += dic[a[i]]
    except:
        s += dic[a[i] + a[i + 1]]
        i += 1
    i += 1
print(s)
 
#011000100110110000110001011011110101100001000110001100010111001001100001001100100100011001100010010101110011001001010110011100000101011000110001011001000110011001010101011011010100001001101001010101000011000100110001011001000101100101000101001101010100111001010110010101100110010001011000010100110101010101011010010110010101001101000110010101100100010001010101010000010011110100111101

然后8个一组转化为可见字符

1
2
3
4
5
6
7
s = '011000100110110000110001011011110101100001000110001100010111001001100001001100100100011001100010010101110011001001010110011100000101011000110001011001000110011001010101011011010100001001101001010101000011000100110001011001000101100101000101001101010100111001010110010101100110010001011000010100110101010101011010010110010101001101000110010101100100010001010101010000010011110100111101'
b = ''
for i in range(0, len(s), 8):
    b += chr(int(s[i:i + 8], 2))
print(b)
 
#bl1oXF1ra2FbW2VpV1dfUmBiT11dYE5NVVdXSUZYSFVDUA==

将得到的结果进行base64解密

1
结果：n]h\]kka[[eiWW_R`bO]]`NMUWWIFXHUCP

然后根据所给的两次加密代码进行逆向

decrypto4

1
2
3
4
5
6
7
8
 
s = 'n]h\\]kka[[eiWW_R`bO]]`NMUWWIFXHUCP'
c = ''
for j in range(len(s)):
    c += chr(ord(s[j]) + 5 + j)
print('c = ' + c)
 
#c = scodfuvmhityhirfuxfuvziiruvigzkyhv

decrypto5:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import gmpy2
 
c = 'scodfuvmhityhirfuxfuvziiruvigzkyhv'
for i in range(1, 27):
    b = ''
    try:
        for j in range(len(c)):
            n = ((ord(c[j]) - 97) - 7) * gmpy2.invert(i, 26) % 26 + 97
            b += chr(n)
        if 'flag' in b:
            print(b)
    except:
        pass
 
#bjdcongratulationsongettingtheflag

[AFCTF2018]MagicNum（计算机内存储存）

1
2
3
4
5
6
7
72065910510177138000000000000000.000000
71863209670811371000000.000000
18489682625412760000000000000000.000000
72723257588050687000000.000000
4674659167469766200000000.000000
19061698837499292000000000000000000000.000000

这个题目考的是数据在计算机内存中的存储，需要将上面的数据转换为内部存储模式 再转换为二进制数据，再转成字节，就能得到flag了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from libnum import*
import struct

s = [72065910510177138000000000000000.000000,71863209670811371000000.000000,18489682625412760000000000000000.000000,72723257588050687000000.000000,4674659167469766200000000.000000,19061698837499292000000000000000000000.000000]
a = ''
b = ''
for i in s:
    i = float(i)
    a += struct.pack('<f',i).hex()        #小端
print(a)

for j in s:
    i = float(i)
    b += struct.pack('>f',i).hex()        #大端
print(b)
a = 0x61666374667b7365635f69735f657665727977686572657d
b = 0x7d6572657d6572657d6572657d6572657d6572657d657265
print(n2s(a))
print(n2s(b))

​

[NCTF2019]Sore(变种维吉尼亚解密)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from string import ascii_letters
from flag import flag


ctoi = lambda x: ascii_letters.index(x)
itoc = lambda x: ascii_letters[x]

key = flag.strip('NCTF{}')
len_key = len(key)

plaintext = open('plaintext.txt', 'r').read()

plain = ''.join(p for p in plaintext if p in ascii_letters)
cipher = ''.join( itoc( ( ctoi(p) + ctoi( key[i % len_key] ) ) % 52 )  for i,p in enumerate(plain) )

open('ciphertext.txt', 'w').write(cipher)

我们得到的只有ciphertext的信息 然而想要获得作为key的flag肯定是需要plaintext

这里可以采用 词频分析 其实也就是类似维吉尼亚加密的方法

image-20250309212510815

这里还顺带给了我们key，只是要注意 这里大小写是不符合实际的

应该改为

Shewouldntwalkrightnext

所以重新计算key:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from string import ascii_letters

ctoi = lambda x: ascii_letters.index(x)
itoc = lambda x: ascii_letters[x]

with open(r'\ciphertext.txt','r+') as f:
    cipher = f.read()
with open(r'\plaintext.txt','r+') as f:
    plaintext = f.read()
plaintext = "Shewouldntwalkrightnext"
cipher    = "nsfAIHFrMuLynuCApeEstxJ"
plain = ''.join(p for p in plaintext if p in ascii_letters)
flag = ""
for i in range(len(cipher)):
    c = cipher[i]
    p = plaintext[i]
    for key in ascii_letters:
        cc = itoc( ( ctoi(p) +  ctoi(key)  ) % 52 )
        if(cc == c):
            flag += key
            break
    print(flag)
# VlbEUNUoZbPyckLSjXLfpaQ

[INSHack2018]Crypt0r part 1（字母替换）

我们追踪TCP流能得到密文

image-20250309220313665

通过观察我们发现字母都被替换了，而第二行蓝色的部分刚好有26个字母，我们使用maketrans来翻译

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
s = 'PMSFADNIJKBXQCGYWETOVHRULZpmsfadnijkbxqcgywetovhrulz'
m = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
# print(len(s))
import string
x = string.ascii_letters.maketrans(s,m)

Cipher = '''
CRYPT0R_SEED:58
CRYPT0R:PMSFADNIJKBXQCGYWETOVHRULZSELYO0E_PSB
SELYO0E:PXX_NGGFSELYO0E:NAO_HJSOJQ_JF>{A2FS3118-0399-48S7-857S-43D9528DD98F}
SELYO0E:HJSOJQ_JF_JT>....SELYO0E:NAO_DJCPX_QTN
SELYO0E:DJCPX_QTN_JT>!!! PXX LGVE DJXAT IPHA MAAC ACSELYOAF !!!

Selyo0e toegba mpsb pcf lgv ngo dvsb*f mvffl. Lgv spccgo faselyo lgve fpop ausayo jd lgv ypl qa $500. #TIGRQAOIAQGCAL pcf J rjxx njha lgv mpsb lgve fpop.

Dgxxgr oiata jctoevsojgct:
- Jctopxx oia oge megrtae, pcf ng og gve yplqaco yxpodgeq: iooy://bu4ifi2zg5etosvk.gcjgc (YSJ-FTT pyyeghaf gds meg).
- Acoae lgve yaetgcpx bal: JCTP{mW9CLVlPjpUtbZFdccPioVV01jdaUeGv}

Oipcbt dge vtjcn ql epctgqrpea.

Rjoi xgha,
Selyo0qpc
'''
print(Cipher.translate(x))

解密得到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
NWPAS0W_CRRF:58
NWPAS0W:ABCDEFGHIJKLMNOPQRSTUVWXYZCRYPT0R_ACK
CRYPT0R:ALL_GOODCRYPT0R:GET_VICTIM_ID>{E2DC3118-0399-48C7-857C-43F9528FF98D}
CRYPT0R:VICTIM_ID_IS>....CRYPT0R:GET_FINAL_MSG
CRYPT0R:FINAL_MSG_IS>!!! ALL YOUR FILES HAVE BEEN ENCRYPTED !!!

Crypt0r stroke back and you got fuck*d buddy. You cannot decrypt your data except if you pay me $500. #SHOWMETHEMONEY and I will give you back your data.

Follow these instructions:
- Install the tor browser, and go to our payment platform: http://kx4hdh2zo5rstcuj.onion (PCI-DSS approved ofc bro).
- Enter your personal key: INSA{bQ9NYUyAiaXskZDfnnAhtUU01ifeXrOu}

Thanks for using my ransomware.

With love,
Crypt0man

[XNUCA2018]baby_crypto（手动词频分析）

题目给了个伪代码 

1
2
3
4
5
6
7
8
9
10
11
The 26 letters a, b, c, ..., y, z correspond to the integers 0, 1, 2, ..., 25
len(key_a) = m
len(key_k) = n
c[i] = (p[i] * key_a[i % m] + key_k[i % n]) % 26

p is plain text, only lowercase letters are refered to.
c is encrypted text

I have appended the flag at the end of plain text, the format of which is like 'flagis......'
Now you have the encrypted text, Good luck!

这个伪代码挺好理解的，大概就是26个字母分别用0到25表示，有两串密钥，长度位置，然后一个作为乘数，应该用作加数对明文进行加密。然后在另一个文件中给出了密文

image-20250312211552469

28kb的密文，看上去是一个文章，但我们用不了词频分析，因为这道题的加密方式并不是简单的单表或多表查询.

爆破密钥长度

密钥长度题目没有给，但是这么长的文章里不免有相同的单词，两个密钥是循环重复加密的，假若是加密了两个密钥长度的最小公倍数个字母就是完成了一轮加密了，而每一轮之中对应位置用于加密的密钥就是相同的，我们可以找一找有没有在密文中多次出现的字串（最好长度为3-4，短了没法说明是同样密钥加密的，长了算法跑步动），这些字符串之间的间距便是一轮加密长度的整数倍，求出多个间距，其最大公因数便是一轮的长度。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
s="ojqdocpsnyumybdbnrlzfrdpxndsxzvlswdbkizubxaknlruifrclzvlbrqkmnmvruifdljpxeybqaqjtvldnnlbrrplpuniiydcqfysnerwvnqvkpxeybqbgwuasilqwempmjjvldbddsvhhmiwkdkjqdruifieddmnwzddejflxzvlswdzxxruxrlirduvnjqdmrhgtukkhgrlszjlqwjrhjqdnzhgrssnhhdcobqytybggxwekdpjqdiwiwrduvnjqdoxknqybgdlienghgrjqbkfdrsqpjqdoxknquciqfrdocpdkwbdppjbocpjqdscgmbbiildpcrzqedsocmnybonkeoycdhtelqgakpydgkwuyepgwfknzolusaukwuybgmgrlszjlqwjrhmiwddmjblohugyrykenbvvhhniwoqpjbebxqsrtcdieflenmlrvbdoffvmpoqvvadomrjjpynybihugysaniioyxqkztwbkctfhqqgwlaskndvvduymisschgrcpuiyrexigsrlibgbqemknjyuofhgrcpuiyrybgkiwzsainqjlvhgtucavjlsqchftefdohfvlrxprvldyfdmrzelflruineympslqubxydvybghgraiqlejeyigarubpvlaorpuydubzbfdljhjdqvldgwoubrhlbbiqidoybrxsflskifryocpnqsagvldssnkvyeruipfyuknlflxrxnywkdkjqdoilhnjngojewvhhzeyscodococptkebfyfieddqwwmicwliyfdgqrwbfkersykinyaonmgrlofkwdcgdppralzkyrmihhgrpsqomybihugyexxqepykpxjqiqihgrpsqompedgqslejbkfdsocmlpwddbivvrdvnqimpxerjscuinlerxzxjqphtewkphgnokpxeybihojqdadkybrqaqyrvldoldybghgrascpnqvldbdewkkujswynmdedkcqhiemjkwpwqyjyrckknldlcriwyexgkvbubhohfvlzxijvldodvljnqsnodvifywdgkvbvldokiubyokngqzxijebjijqdruifkbscffdujpuydubzbfdljrojuwkdvmdljpplbwdkgfdidpgwnpkpxedljcqhwwrhojwzvdonwwbkkzdubrnldjjknlbxlrxoaorrpnulikawuwdnhjqdnzxzuujrlnrubknluokkqsriawhffzqchjqdyckhdjqzbmiwkdkfnlkknlqvldotqioeiprrsqhgdljrvdbwocphdzgdptkebknlayblodovldxnwwkrxzflebgmivldpjjcocpeewofgwlasknmiwbrugycocpwnaruifvlruvlddkhjdqsqbgmiyruqtbybgblrvrukmfsovlnryepgwflruievcrzbllmpkdtyrquqiuyupvarzocpjeujgllybqeiyjcychgdvephgrjqgelxybcqmbkokhlesqnhnwzqqixyyurkwucyqidopizhenumplbvxichgrrocsfnpruiwfzqqiprsvqkwxwsnksnjuzbprwrrxzoedximooncifbukpbdesiabyrwjzehrsqpotewrreldkczveflekqmiwuztltwbkqsxeychircknawbybghgrmudkfvjqkgprraigmyzqfkxiubdonqvldgywurkllkeclimblibhlwzudndpkihlepwqeiytwqkkmybqnkprxnpwldljknlbyudhntwkwkxrukcqmbxojiqrvmdiwybqdkyybocpmiwkhxmnebdmgnzizsfuemcbynsruihfljzmfnpruipfzgvmjjbyfkwfvarojeufdvdozsxnmeobcgwlpdzemiwqyimrjbrhvyeqkiyqurvpdqerknlbxsqgmbalzphrznrxmiwqknlewbeypdllrokdubzxpjaovhdybquqijkskyntwrpxdybqqjnwidrejqdspobrdlrenbvlronqdqdpmiwmpymnvldndwmcrhvdljuifdujaqiwemfijqdazahfznqijxbruignzajgmjubppjjybgkwfilkkwuuxzlinaqgnntybgmlpynlietybvpjjcocppdlacgzivkvimpwjrpwnvddkxivldndwmcrhvdljbnjyaonhdtmkhvkeukdnlawcpeldleqyhfvlfiqrkoholiwlpppfcndpprsoliprelxqeybqwvljexknlwuiciyrmihejzwruiydrvrhpjxddydqwupywnvddkxivldpjplkptlamruikdvlzbmiwbrugysauqtbwkpyfyeudpdqeriijswudbdebqqiepwniovnodwkfyybghgrjippfdmkkqprkifijqdxzlinaudbdeuofydvjxhhtewocpnbyakqqnvlfygnokdkwuvldvdddsukarliwkfyliqnjswspbtyoddgsfcrpygrjqknlewsnkznubxgwtmkkkvflepxefpsxqmiwddgfdcrpynqiscevlescudqzaiqarybgpldvlbgiwklpxzrynihgflenndpkocgincqaknybschgrnynhnxwialnowmuiwybqgvldskzbmiekdmgncndikvxicbldvldvfdjqcqmtedddldorrbtwvlpxmiwjqijtciahgncqbndbzqdjtkebknlrydknfyjoculybqgiffjqaqyxwdkknqxndkfvjqngfdxoqhdosawknqcqeiwyuudogdhqrplbxsnietmkzaiybqagybvrrelpbqcgfdaldvqrubxelrgrukmbbqfgzivokhjflldgzivruifrkicpmfsqbnlqukpmgrjnrekflemisnjqknlxjswjirdruimiudghntwmuiwbbqbkflufdxmnklzqfrrqkmlrlruigdjjpxeybqdkfjybgogrklzolybqdkfjvldbdvjruhntwmuiwbbqjqpturkiedadzxzdljjqpoedkieiwdniiovlphdybqqojwcijqpturbvdqiruisfpruhntwmuiwbbqaqyaeddbdeaqpswrckpxedvrqgqvvqgnlexokglqkqkqfyjqcumivldonmvlkgpraldxfiwjdokfcqghgroeigwrckzbjoycdkwugbdmwnvrukmfvmpodqwianleemcejbgkpxeybqniarlruhntwmuiwbbqnkwlykzxznppqknbwocperwudpnyyfrvmvwspenlliqkwyexpdfnzykimeorudtyuofnttrnddloeddevfibzvjqkqpxeybqqinqzsdopjbicqydljfyyraoqpmiwddgfdcppwlawrbilqsocontyerxjyuickwusocojyvorxprlrknjysovqwwmvdhydhqqoluraugfwebxgwlxoqkefcqromiwdddliubghgdvjzqyflruiwrtrqqdtrykggdhqiqfyvldsljxqqnjkcsukarebiypfcnpgefvazajewvigwuybggjtdqpbjqdjheqbendhtbvihwgiybgojqdycplecrpxeybqngzquxrwjqkqzbpdlsnxdyubbnjybqphmdubndtyjoknleubbnjybqiqwlcrzkmyyscodtwiaafdjqigbrublkwucifiifgqwkkrjocpnourbiyrlikbdevlddidkgcifbexnqprexhofnsqzbtbaihleawjheqdljrbnyaqqiwnvxzvmiwmugmrlqnodocifidooknqprexhohnongdlazscpzfhqfijqwoqkwuumrlilufdydvyfzgxreyqenqdsnkfkebxidvjldkyyukpomewofgffvbzhfyjoculybokedbviaafxbizolboclgwljoknlevlpxyvlbrxzpbqcydvzicusnjviifbubxomiyrvqttyacqmqyudkwualdxvnoeqglswgcqhflecqmybqjktbwruiwfljdiejeypvlljibgwlasknjwzrugwlcrukmljibkwujsngwlvibkyumihvzewokiybwnamgrlicinbddhxbpurukafcszxgrdqdefiukaknqvqyjyrckrqwnpskhgrhqqyhflqvqtujscshflqknjymihejjrqrxmntsjkmrdocpnujscsmiyrrhpdmkzdlesqavdtvlphdybqqmnqwmuiwtmchjnbwuwhvfjqngzqsaniiovirhfrspkgwrckmampbqcgmfclplsoonigyrcqchnyclplsooncifbvldvldzskydovldqmiwdwiybebrownvscmgdvldvlswoiomnmihdtyubbnjybqjkwqerqiarynkqvnoruiyrpiqinomihmdvzjhxerjkkkwubsflnbvqcxdyvibnjybqnkvbrykvjybqqhdpboknlueqnxdycovnjwpiamgdvsnkvfcudkwfleiifbrykgfdmskodybokhgreruiyiynaejjjqpwgjeypolqcqzbgvsihvnbykdxfrexwvdkedkgdqsaiqwrzscifbaonddelmuiwtwbwvjfcqgevyynlkmfhqaktwvkpxeazofietmkrllqvfrvmvwkbnlqzsaienwkcqmoubgkffledvmncscugrjldkyycldjyndyjifdxlrldbepuiyyekwijzbqqenqdokvtybsnhdawgcqhqynbkvbvimityvqqiebeudhntwkknlewoigwvcsnonwwbkhgryctanewjromdzgphnswruianucdqswuxdgwtwcpxwnvddkxivldijeexigsrubvqtaoriimvcrplbybokmltyacqmowqildqwnvmgrlrbqhnsqchjwgruivbyacqmiubxmgrlicihnsocokrygnogrjqeijwcoildozsaiseeenejjrqildpzihplevlpxqvznndtyvldyxdlbzheeyeknlkzihugflruisfwngxdyvyqxmiwmuilwexknlpubdjyrckpxenpruinecgrxfjeyjkwqerfkbrclzifnlnvhgrdyfdlqhaknlyynlkmfhqrbhflrdvfieyipfdmkwvnqisngwtmldkyyalzmdvzjmiifwfdmnqvqqiarjaniluukpldqiscufieyipvnoddkiwmiwiwjeyqivrcocpfrwazahnongdliengydvjsfkzrubplifsoxifdljnndvzjvqtnxqcydvjqpvfdljigfywbvqtpeyipgrydvqteemctdfkqrxjwzfzgxrcskhjzwkkmdnpynhduukjqarjrqamiebdhdvvrdvnyybgqwrvihxerjkkkwuurkndvilknlpyfdqspedgonbpiqiarjywqwvcadhdvjjdjmiukaqyrhqqonwwbkejqmogqxyjscinbzslijpubgqhkybdmlbwqkvtybruvdvilrhqvvskpnsujdotbpdzemeoruxdpzqkafkzovnnuwocpfrwgnndvzjvqtiujdgwtmldkyyurbqtwdbzhqrdsabnxonkhdoubgydvrykognongydvbsgiqrbscpvnodzmwbbqilmiwbrhhnongdlvcqiifbpiqkwjebdhdbwqlydvymzejqsovtlfzldvsdkqbgmiykfgirbibxdazqromiwkppgrydkmgnaihlebubxkunmihofnlebgminivqtbbqpvmbbqbndpeyiptqdqqomdljpmdtybzvefckdwmlwbrafnjkzlarvldevbvqqydocsiiwxwsnhgrhqqypdlmuqhnongmjzwxqqpdrqpamfpyipyryukqffvokkqewolbjbvrpdirumzaiuaoishfvlpliybinihiemplbfaihleqernhjqdkkgiwvibkmxbruikeecdoffebwkfbubxdvjeyzmlteddhgdlezleyelrehiekdvarcazazfhqugpnpazayiwoqhdecqqtliuuckvpwlptlqerigardsctjfllptlybqvxdyryrlmyemdvfnpihvqnlqnllyokcqmawppvmfkyikydljnixyuickiybqwqlycurxedljknlbkiqjnnlkkknwjsninqinzvvojifhgrcofildjruiarjagvjlebxgarcvrvmivipomlwiqulpbinljjcskhyrwkpvlkeqfomiyrknlrydknheurdotkebknlbgabisrznknltdibxjqdrhvwybqfgwyeppjlevlphhrsovvlxedgqtewuwhnqwknognongydvkoqimnadrhldljzxijvldojflrnswnamuyvnokuqtwdazapvcrciluclptlzliblluiqpxedjrpxetokrwmiwgcqhwwjxidovldetbuczbhnjjnhgrydkqsawscujevndofdljknltyerwdoziegwlmihvyryjdvfybqvpnkvldgykwbngwnoduijevkpxeybscsmiwapvlflkwgyrdkuqtwdokvlradrhlfvkpamnrszuydxlvgmpeyipwnvvdawwugdhgrbsnhdemiakydkqrbnpwddhdxbizolawrbilqvldjdpwdzbheurrxzdxidejqdruilxcrpovnpowqltobbvnyvqcghnongwgnekdhgrwcnhjbmskgfawrkiykeqkvvaorvqtdljplitmbdgziriqojljqdhgdvsplhdmkjndncqmkewmpzimemsnxdyybzjnquiciokjqnoluurrojbebxhgdvdrolbpdzejazqdpnqimzawuedpopfzscupnorumdedkpvlyuudllbcazafieyiptyvqqhgrsiqmyfvqknltasknjzliblluiqzbmiwsqhntwndofqwknkknwrrojuwruvdqwjlgwlcskhnqiofqwlvldkfiwkzbgfcppljxwrqynqirzbjbbszxjquupulnorzbmiwonnlbxidhyjukppldziazdjybgjjflocphnljdvhfvlppjbbiahgrdsjhnnloqynqhorxfiynikknwrnilzvldedybqqqsybqnqwlciannbbqpvmnlcdgfdujkqjkeqkmlbboilwnvgcqhjeyqmdevlhxmfzazaefwocpgrybnmlewjnkvflevifuwoknnbynbkvbvldvlswoiiydljrbnqdqdpvnomzaiugbzmpjaiqhgfvsnhgdvsukarsiqinqsauijevrukwvxicevyebxaldljfqyrubfyercsqimiybrxpjbocpnomihonqiiadldorvhgnoeukinlqrxmiwldkyyexknluwkdvmjeybgiwboeijqyygglqkqwqlyjarohfcjzemiyrdxxiybkomiwldkyyasnpdtukwqlyjaknjycscufflruipfljrbhrkihlerlcukwysocogrydkkwuyrknlbyudhntwkrxzfllropfljknlqubkvtybldmdvzjigarubknlbbogqhnpezpnqcprvjyuicmnwzoimjjckrxzflkwgydvszxhfznciarjqyjidubbidovqconqinhlidrsdomneyqwgfzjqiwybokmlnodniiswkfkvbzqdjjwzihvhnjjnkyrrykwyvsvnhgdvxpliuemcbynsruisrykkqsybqfgwuvlrxbflerojwaovomiwkkapazscufyebdhdkeqkvvdiddkmbubxiyfcldmgncscufnodngirlcdognacpxvnokrxzfpazayteyknqrpsilluasknsnejuqhbboilvnodukwurqqknbwjrxqwwkngwluxrhnbpsilluasknznzjknljcovhgrlsxnmflepllkuqqwlbbsnddbeubgmiyruqyqaldxgrcscufiukiqarcicufndibijwzlzmlwcqnndvzjbifflexiwfokroqvvoqqqflknqwlyrknlawerxwflezbjbzibokeubxiarlruipncrbgwlwjnjneurjkwqerdoxdxqwnvbucplwrkqnonymofketybrownvndofdsyngxfybknjqmihqytmkdlsnlnvhgrubnhyvsqchdqalrwgiwpikvbukplnyvndqtyexkawrvldodqirukmwuqnonwwbkgwybquijeviakpnvldvfflenaknlruiifxkzbgrjcugiuliiqwlubxvltyscotqpyibnwzqgggdhqciarjoxvlrdmrhgtmiknlecqibhieniymiwrqamiexknltyrkiybwqfomnzsddlyaqdxtbmihvdybqqolwpsnkipyanodejaaqyjeymamjeyqqmiwdniioidzmfnlkzvynakzkiwukbiiwvldvlfcbzomeoexllnpkzaidljmqejcoeinqvldenqdkzbmiekdmgncqnqtwcoqijbzqdjjqdmuqfrrigglbyddqtyexkawraldxvnoddkxivldnldjrzbifpqvqtbboilsfljmijvvarxjwzrugwlcqeiwflruiljwkknjyydddifljkqqryykyhrzseidqzakqefccztlerqpamjyniiibwsnksnjuzbhdurrxzbempolrdocpmiwqpvmiasilvfwngydvyxiqhrjjqijtmihveewofhdybqnsvdljrhhfznmvnqiazavnodmiinhqghgrdqegiuuqghgrhqqyedmazahrjqmqyqlibydvdicqmiyfdhdleruvdviluiiwvifilyybpxzrzupxvdaifkwaedqqhbyupxfiwoqharjaaihxeyipknckdoffvsaydvaihlekeknifbmihetbvbzhxwysfmgrlofkwbbocpmnocuifybqukwuexpmdtybknljriknmnocuhgrbqpvmnpqkiyqurvldswsnhgrhqrlqrvmdiwwefdvjqdnztlewfdvvtybiqarcrbqhnsqchgrebdgfybqjvldvszxdobsngpdisckmfebpxeybqzhgrjsnxdymqkddeludxhiejzxdypiqunswmzelqvldgywurklloyyihfpunixlswddxunmruineiddkmsudkalbzieimiyrgqlblikvlqwmrhfrzxdtlemjpyqrkififdbomgmdljrxmvjbpoidhqqyinhqqoltrdpwlybokmgfklroqrvmdiwybqfvjybqqhgdlqpwgnvldvinhqpxeueymhgdhqciarjvdiwnlkwijzubxhleskiqarukpmdedialnlbrbvnyvqcdvdbocpdozsxnmvxickkdiqzbifilkbyfwbgogfxsnkipyankfpwqkvlbxiconaunrhvqwfdvjqepwqyyobrhvfpazaenlikawuwdnhjqdazayojsdxevljdvjwzczxefvszxfjeybgiwlqeiyvljdvfyybgnntmihvpncrqkefybkujesqchnbexknlnvldvkrjkzxfpwoegwlmihedbvkptdemudkifcrukmpbsjnvnoqphjyvldqmiwdwiybebnhjazqvqtesinhxnsxzvmdrnddluukrxmiwiknlexqqodqclzafrlibhlwzudndpkocydvcqwkydvqvqtecqibseeuknlnvldvkrjkzxvnodfgwuybgeviwoqhhfznciarjoxvlrobkgijeyqenqdcdkfrcrzlnswscxttrqqojqduvnldjrrxmiwurompwkukiwlqeiyvljdvfyybgqwrybzhgrjychnwaqqievkqknlwybxajlwrzolswbbqyuclzmfiynieviwoqhqrobnijwwjhxirckrhqrrdzslqebiyzewokodejibqyljqphunmcpxyrhqplvnodkvtybsaydvaihleawddtldzqgydvsynhlfvldvedlcdxjzwjrxmiwkhxdekoqvvjeyqwyncknndvzjckmvjquilualphhrcovqsxebkiwysqchwnjseiypeyipfrwgknlbwopxeqemrxmrjmzaiuvyqxmncpqgwlclzaiucldnlrdoilhrcovqsybdrbmiemfkwjexhohnongdlajqphgfleknnbysqydvcqddtymihvfiyjzmhiwbvqtyodcydvjvpwbyeruifvlazajewxqilawxzvlybqnawnpruiedmocpsewqmisnjqknlbvoqodovldxnlbrpxejeypvlojqdmgrlruiyrukcqfvlocpwnsizxjqdbzomdjazajewqeiwojqdmgrlazaxwekdydvjqvifvxickiwvldvlfcvhhvnooqijbzoeimnbsfmgnsazainhqmixdokdydvzieigfsocpjbzoeimnbsfmgnzieifjeymixdokdnlwefdovnomdkyrynidllioqojyvldujywiahgrvqfjirybgijxbicidookqixrufdogfckukyrexknlaeychvnpruibflebnlqbqdxmrjkknlywuwlldljbnlqbqxqlbeykdtyaqpvldznoijweynqsnlqpxdybqqmgfklrojqeruiypyazbqrzskhifleknlzubxydvkocxdykicottwvdydqdazaydxpdhnywruidybqqnjwpiahgrzipbqrzicufyeruidybqqjlecickwuvldvlbbihleewupgwdzskhirrddkeoedknlxbocwlloqnhnourbiyrlikbdemihvzvwkkojwzlzafrcmzaiurqxvjswknknuyeqkxfeynmdwprzkffspiifiwqwmnwzazawnvlzxdeeyqndvcqbgmiyfronyybghgrcldikdlkbiyrdmdmdvzjukarrqdxgnliqieyefronymihvgnokdgsfvmdvlqerrxvnodnhdtycugfyepwietmehifyebknlybddognzjpxebysgxjjaswiwnvazayowqkkfjeydxmrjvhhjbmihudnorxiwrjingmjukcqmflertnqiudhgdvmugxiubdieteddhgdlazaenrykgmfcscunsubxelybokmgfklvqtqwqgedewrukwfdivqtdjqrxerwjjnjeurpdiraldxvnoertldljbnnwwertnqirhvwjeyqbjxwobkvberukmjeyfkvqernilybqnnvqwknqsybqqixrufdvmiwjrbsrjqcwlawrbilqvldvnxbqnhpdlocpmiwpzqyrcrroqvvogkvnplhxzrjocpjqbihvdovlrvfyaqzbmrlvzvynaxqqpnodkqpnjdzmfyeppydvjjddmbvizayjwkkiyuyangmneoftnburdpqjybxiibybgplsunndtyuedhyfdiahgrsmuiwfvsnkwdledlnkjovkwnzjwvjjwdpxeiwsnddewjbnlqurrojuwfrlnxeufgmdliipfflocpgrxonolbsqmyjovqqkiwvlronblikkqddpqgfnlvhhnuebzhifgqknnbaoilqrvmdiwtmcdlidljknlqwtkjyfciciybkqilvrvspofvjqvqtybokgenlikmnbbrzvlkjipwgybqbkyuwdcqmybqmanwdqqqsybqwvnbebkndbwmuqzfhqvqtdcqqjlqvmuiwjeypoboedpbnbbupygdhqcqmiubxdtycqqjlqvkkqzfhqrhnbvldxzrlqqqffvazxmiwsqjjevrqgxzwdvotxkqdpfbeudhntwkmamfvoimjjcczepfvknanxujdydvyddhyvzapbdeiseiypbqcydvpiqunswuhverjqqohiebdtlecprliazizpmiuqeifpbiciarjkkijwybglndjkbndvvrdvwnpoiolieignlpbijkwkorugfoubxiyvxichgdvmugxidsegercezqeojifiafzsnnlpbijkwyeyjnmiwfdvviwuzbmiwepvprlrzbzndsaydvjldkyyukptdwkocqgnakukiwmihiokwckbinaqqomnrnzqpflazayiybgojbvdpxzrpiqedocqibnqdyiulqkqknlewoqimfsqnmgrlsbqtwdvdmynledpjqdcuijywjknjyuupyidoeukmybqdfkrlkdqsybinihierugwzujzxdygbzmndsvdgwladzxzrdocpxiwokiepbokogdznrojjexugppbiromiwphvfvwdwljjubxhgrxoqhdovldjtecydpirvlrehiemrjlbbsnodfzqgnjqdkbgmimihvzdjudxmyygdydvjepvprlruipdmbdiefvoxknqcyqiijmihmdvzjcqmfvsnkkfvaknjysicivxboculeccpxwnvvdudndepverlqqokwwonienlikmgfvqbkfimihvnqbqqiwypohlmbasknvnodpwrvuddpafjrhiffaihleiyfdhgrpohlmbvldyjewnrsltubdqhqbibqsywbukaruokhyfrykieyeuvolwpcqgprcsukarlqeiyxeufgmywjnqmiyrknlnvldvkrjkzxpdmxdiixeuaqyyyviinqsawvlbwbjilswbknltyklodozsaijewupobbexgilkwdfyfywdvydvsovztuiqzhgrjkzxijycjqyuubxhdjeyqswnandpzrexvqtecqibmrznfiwnamuqjtebxaffcehgiymocphiesnawlosihvybqkvtwmzhomfcldmgnpqdlfiynautfzrvqsjeyqenbdqdpfnlnvkwfdszhjqdoxiwfokmvldgupxpddqikhbybghgrmoqimiwbdkyrcrkqmiwldkyyexxqefvsnqwwmmuiwjeypvlkodnaluvlphvnovdwdtwkbgsyulptlqeqcipfwkzudurykgsfyukqgdhqpxlqwuvllybsnomewbxhgawqtajwvifgwrvlphmeorukinlqfkvawruiafkrzvvnomrliawwhgmrpdriwuzabgmimihvlqwuvmgrlazaqnvlgglkwdukkbyupxpdmczepfvkhgxfdqrxfrzxgisrlkdldqioxqmiwddlnswjpejqalzmjbkdhwnouqgbderqrxzyeiiqaflepxeyeiiqadrndkwucrqkwlwrzvlwyrdgprvlremijsjivrcrdvedmruisfjkkhntwldmjbyklgwlypzlnxwupxwnvrzhjzwowvdbvskamrviwvnbebknlbwczxeyuudnlpykgvnqgscuhflqbgmiybzamxykkkwuvldhgfjjkgprbqbkfiyfrxzdpsnhsfilkmnybowvdterdvnqcsgijxbyqwgfpoilmiwankvnpezqedljdtnwaqqimeoqknlqsaigsrukmamnlqiqwlkdrelkurvgfaorukionynhnxwruidqzazxlpbiukfawqcawcokkhdtwsnhgrebdhdpbiniqeeruiyfboeiqrwbhxuvcrbnlqmiholryupxirdrzjyfcicojjubvqtebqpvmtyaukkiwsnifxyprxzojifkwdjdzmlexdrodqybgmgrlazafrwofkwujycslqcovgwjeyqnldjrfkviypuifnoeuhlbkowiseeunqprvlrxzbvsilpnjqhxqryykgsvziahlqvsfiffboeigdvqggwbwnaplowbniqvvsaghrjqnhynledvnpeyipwnvlptlvcqgotxbobijkebuqhbvywgefcldmgnaihlekyrjnmiwlphyrdscnnbwadohfvlknlbssiidobsnlnkciclvybiniqrlqphgtwcpxlqhazvgdvqfiniyfdxlswdmilqwbegluliqnjywjrkpdrieiwnebdqwwmruqfryvztltwcpxkeysniderqigmyzqfiniyfdxlswdmilqxdpgfrdbzvqrzskhirdspeqrzibxdnlqvqtecovgwlvifinuebzhtqdqqomdljvqtfcpqknbwvdydqduvmdevlpxedlscotwvazaenlikplbwdeignaudkwdssbnlqzsaizfhqnellengkwuuertljeyngiswdpxejwrrplrsuvolwpedxleeynmgrlazayrycuhgrbqpvmnpnrbljeybgiwpscpvnodniioliknnlbqqhgdlruisrzickwulikldpwdknjqvldjynxldhfyjoculybokydvclzaiuxskymiwkiqhoeikiedljcqmybqnldpsscpluybghgrrnrxermqgvjybqqhgdlruiqwubgnldjrdpnyukbgfrjxzvmiwnpelqerkqqewolnnbkdhhxiwkhjdqvldnlddiannbwbdeviemmlnqdsnnlpbixgarcazadvviannbxijslyvlphgrsovhjzwihhdomihvgrydklnowsnkkeecdoffebknlbzibqsoeikbnqdkrhmnekbgsyybgnlbvqwodvvocpmiwkbgsyexaqdypscpffvrzqfwempxeiwrzqfywpnqtyuxknlewsnotxboknnqiononqcifidookjqpturrhqdkgbkyupiildpubxqtepiqisdvldvfoeikomrxkpxebeudqsvcczepfvskbdeaoqpqjefdvyvzscudvjcugiujqchgrvdhlvleiggfiwmuqnbebdmnyboilmiekdmgnyddplrsqgdjuaqpvldznwvnbebdvfaornqprexhojewscwlwzkbgmiascpdpcocpfnsqbgmieykomeybximiyrbijwzjdblqdihvheebxohfvlfqyrhsxqyybocmlueihvyfilkofieyiphryniwdqpqnodvjkrxfyeicijqeruiypwmzaiuyniljvilphdqwocqmiwdaqynodikxzexzvnlubplnymkuqtwdmdkiwjqeijweyqtnevydohraihledzkzljvilaqyybqnkprkoholdlscpnsujhkifcomqarsocejuwnpmfvlrrlgrkifenycojvntwoxknqcrfkwtyjdwdqhqchnnlkpbmrjrukmiwsnxlfvldvjaefdkwjebdxdezibiyybockwjebdudswdcelqvsnkwdiddiprlrmimpwqcydvybgevbwnaydvybgevbwnakyrexkiwpjicuxeuudgfruruiydliknlelofidolqdpdeybpokrkrzbjuukdkfrukknlewoxvldvqqbjvzrknjqrqrxzxebnwnnokzbmiwiknlexqqodqcxpaiycsahgreruiykwdnqwwyyxnfdvazavnocpxkfvaugpaorrbvnonpaziyrugpjeyfkvqwfdvsnjertljeyqolwpsahgreruiykwdnqwflzhvlbmihydvsovbdeiqkhgruboayjrykgsjeyrxuvjqugpjeybgiwynbkvbjqfipawdrxmeoruhgreruiykwdnqwfcazaytekkolqcskgarcqibzfhqckwnvldvqndauqhiwqgllbcazajewmuiwjeybqtwdlptltwbalvpuruydvjmrxzbybgydvkocxdywfdxzfhqknltyxdkmiwdzxxryupxfdvokevaeoqpjqdokipjrddkedljgvjqguvmnqwocphrlrpmjjzohugflephprvldxgrkofijlyscbderddkedljbgwrybggfkodcieiuupxeybqpxzrzkiktlbqgkmtwlphlfcogijuvlrxzpbizbvnomzaiurqphdtrskgfybquqwnjiahgrsyqplewjknjybqrownvruipvjjdvlevldhyfrycidobyfkwfvaronqurnonwwbknldjrciarjskomdzgphnswurxeybqvplrsudejurqjktbwsbgiwlikolwzuvpjjcxzvznzjpxefdqdemiwufkeawcpafrvldymiublevuyannjswowvnxwruivbxddkeawxzvlvcruinejsjnlbexxqiuybgonwhqqqsfhiqyjqdqmqwjybgmlbxddkeawxzvlybqfqtebqpvmbybgqtecprvnycocpvrvruivuwqfhgrskdlarcruigncrnkwuokknlloqnhffaihleqermimiwndkfyyuzxztwbbgmidddkpbybghgrdqngyrviaaiounihgrsdphgrjrukwybqxvldvqnhhfvlcqeewofojqdbzplbuddomiwuzomkurrbtwyuzxztwbrogralzhtelkugfujqpefflrzonwhqqkwuiiiphryddkiwknreqflekqhdjjknlboufgmnpihvgrydkoercsqifieyipmiwiknleknreqrjkkijwmihvfdkgpxejeyqjtecqpxepytakmnlruidqwocpgryfvqwybqzhgrjazafieyipkfvaugpybqjlntrscuhfznmigdjjdvsnjlroswwkukwuvlddtedqcmnwzupsliukbkvwebxiydljnndvzjvqtflazaywwocxlbckdigfcxiifixyabnqiywmjedldlkiuupomrxskmnwzogpmnmihvfpuxkxlbcazaxdlbzhuvdedkwjsocdljebgydvjgcqhwwjxidobsfkwubibopdznrovnodlxdpzqgulfaihleqerigfywbkqjxebtaleedwvldklrxzyeruixnlwhiyrdruimeonvbyrwupxnbbqbndawoqomiwnzkenpruiqnljnljswpphnrlriyjybihojqdadkybyezevqwsxnqnjkpgeyeudggdvqigsrpiqgmfcbpazivvhhjybscudoxorxjqdadomrjjpynkyknieamojiprvqqyjqdkpmifpqgkwxubxaknllrozeyfdomeuxdgwqyrhvlfcvhhefciqplezicunqixzvdedqqodwurhplfcongirlrnhdesrukmajqpsfuemckiweyqplddvqkwxbqnylyurniwucihvifhscuynernplrxqqgwyeruiifhscugrydkqsybqigafledkyybicwlfcpzslnpruifryrzkqeeilkwuvlddynegkndvilkelaorpxntyerxjyufdiodiedvjyedpxenlcdgfkegdqsdrdzqbyeruifryocpmiwkdkmieyxnmtwvhhjuwpqixfyrrtluwxpelebibxjejibgfybqegffebknjywtplmbvlddtbmbdofnpruijqvomqarvldonqiscudovlduydckuqkkwdknliueuifyhsqhtrbqqipdmvdhgrzqpomflocqmiwdbqywdruierwppxeybqugziiikqmiwjdjmiedkqmiwldgzivsckfyjorugyzscidqzaknlbxojgdvccpxpnhqrxxfjciiffpskmlewbzhsnjihvxnlcdjmfebzbhrueuhfdljfijboddohraihlebvocpnqymdqsybqagyrpnvkfpwjzdloeddhgrcyckfxuqchnbvmrhgnorrejlubphnnlsnkqvvcuiypuruptwzgcgarcocpdvvmzvwbkoiifaorbnjyaihlejeyngwxwmdkyrlikkiwhqximdjspxfpbqcydvcscumiwlhxzemldkybmihmnyblrofyeupwguwoknnblikxldjqqhdybqpuluvlpxmnvldxlpriqxwruruiyfcnrblfpscplrdazapvcrmixdljrpqrkocpnurqpamfpyilvnvldvhfcqlilkcsiiwypiqhgrjqrojtybrxdvjbdgziriqndndmuqnbdarxztyaukkdpyciydzofqwlsqcgfdaqgpnqixdkfyyuzxzybqpxzrzkpbdeiikhlqjqplnymupyefwocpiryfdgwfvkbgiwcqeiwybihojqdojhtdzskglbybgbjxvkkqqrcpdxmflskosvlqqkidljknlaosipnqiiakmnsvrxmeorumlyynlqwwmrzqtecqitlbrykodtwrrelbaqkkizzihplqeyxnmiyrzhgrjkfkviwoqafybqzdafeyngfybokmgfklrowrhqqolrlychnwcifidqwqyjyrckdonycsfjijuxknltunlyhdmmdvlqerbgmiubfignakuqtwdsukarcqdxnyedlxdplskawwwkngjtypuyffkspxjtebxjgjcsjgjqcruivpeyipwnvvdlnrhqknjyuofkwdcrqqwnsqqjlebowomiwkdkfuwxrxnyuicqsdcldlifcruikrydijlebowomfsqnploubrhnnliawddzsnhgrdspedqdxpelfcruifiyjzmdoxononnlkkkwuubxgwybqigzivoqqdyukpbinaqqhgdvjroedubnbjtwruiyrukcinybqqvlwuerqwqednwnrlcddljebgdldorviarjaxvldvupxniyfdswnabukebeudhgflenejwzscnnbsolitkybggmpykknjycuplibeudhgflebnnxbpqiarlrdpnqyckgafvazvpddbdofnjkhgxfdqknlyjyiyzewokejqukuihiemzaiusonhlelizxldljbndpeyipqrsonhlewjmywnlqrmdvzjcqmawnriarvlphjtybroprdszwyrcsfjijrqjktbwldsnwzkknlxjsfgwdzkpxeybqwvdkbqkomnzqqkwxwsnldswkrwbpuruhgrcsjswrckzbgdoeuhnqwknmdeskbgiwvyqxqvvsngmqernhydledhgdvqeiwrzqwnjqvkbgiwmsdleddsnkzewqfiwysovdlybqnndevqnhxvvvdhhrwbkmdtubgondsruiswyudkwuuofhgrddvdtbbocpdqwppvmnpudwdqcyfifybqzhgrjppvmpwoqijwzkdibfleknlboufgmnpruignzafqtyyscdtyclpliqerzayeeogdlbbiqhleuxbixnlkrplevldjjbvojnjevocpwnvoxanuwmroenscdkfrcrzdlpukgqppbqcgmawczelbvizjynojkqhrwpkqdljoeimnzohugdljkqdbwnabtwvinilzeruiyybocgmbwnanjuuxrlirduvolwpmrhgdznknjymihswnamukmeeifognongggdhqaqydznknjymihpdqerlxdpulptlwwoqxlucsiiwxwxqqpybqkkizyrrtlyendvjyuicbynsruinqviiiydlrpxezubgxlbcxqqpybqhxbfljvimbvdpxzruofawljokisvzrzhgrcqkijxbqqojauezhnbykkqwrzqpbdeyrzvmiwkrllqkqzbmiwqctnnokromnebzgfjaldxvnoddkxivldiwuexbnjymihognongswnaazahfznmijyvlddllubcgwlexbnjymihognongolqcqpxlmyexiydvszxnbyrqamivlphgdcnzomfvkkipkwdrbvnocpxfrwiclvpboklnlbrqiarynnkwubqpvdqzabnjycihxedlbzawxwkknlqubkvtybazaenlikolrliqpdjeyuijeyxpwmfcokvtybycolmwjvqtxybcqmwyyxnjqdvdawzubgkmybqnkprvsfimiwbdkyrcrkqpjbqpvmdjqpsnqimrhgnorpsnqijzejqdowqdesocmgndidownvgcqhiemkqqrionnvoysiayrukcqqwwdknjqybrepndqnhfvkcdofuuepxvpbqqinqvldijevlpxejeybgiwpscpjyjqpotewiclvjeyfafydsxmnybruisduruqsdxqpojqvkpgedbychlupiybdwzibieamrbiwymlzvfrsqckwuyppwbnprbiwymlzawuciawdvjkdhgrmmrlizunielaoruqhkeiqkwubibomvxsghgrmuhomawkhvlwmskmdvzjcqmawmzvmialrlloedkmlqvaaqorcdrpnqiichhrlrvkfbwkpxedkczekdlsdpqjvmdxmjaiitlbvijnjbwocpbfznzxltybrhnbvldenqdscafybokynrzjnhdybqikhbsogiqjokmamqwfdvmiwkwgyfvscafdvdptlwwdpendljpxjsuephdeybgiarjagkvfdsnwdswdpxlpjqxgdqasknnqsanqtwymzejqxdzhlbvqgojjubxqsxeyqolfvmpojeueuhlnokbkytmkzxsrznrxnyukpgeyenrblfaihleiwoqpldvlnjldgocpifpqqknbwjuiysesjijwurklliueuiydljnknumihnldjlrewnamuiwjeyukarciitluynihgrsanhleuqnqswuxdydvzicusnjjdkmipiqgmfcvhhjqeruiytmkkiyjexigsrrsqhgdljgijyboqimiwrbqwnrndomrtpqifbuicodordptlemuvbyfwbgydvybggfiynivltyscomeybxiybobkqifpqpxevlrzqwrybzhgrjocpldklhxmnbsfolwpychnwvldpjjaldxvnokukiwcpdkbdljrogdznigfywbgiltubxydvjfzgxrsazmwsesjijqdmuiwfclplibvocpqrpiqivnorugwzubxevbwnaomdljrxzawxzvldssqvdevldyfdmrzelbbihlejeylxdpmihvfrzxvqtpeyipbqemplitwbpxefcovqwwmmuiwfcqdsjwzudxfiynigbqemfyfrzxfkwfcrbqprlicinbympslfljpvbqwknhgreruiyfconllrxsclnlbrpnlesskgfnlqbndewbzawxwkknlpedipdopdpuprlrnhgdvldejjwboqvybqbqywdmuqiwmocphfvlzamflrdvyvxrrqwybqqiifwkpuyrwbaglwdvdhhrwbknlbklzljeybghgrxidhfieyipmiwkjndwydjvdbcsknlawczelbymroltybnndvzjknlkeqkwynckrhgrrqjqprcowvdkbqkylbvqqiarukpmkiunzodkbqqonqvldejegqkjidkqjkyemscumiwsqnlddkrxqdcgdhfdljjvvflepldvdmroensmroensxzvfdzqwqdexlrldbepuiybvldypvcrciluckdliybqrvgryjnhdowqghgruduijevknknuypuginciwnlevipomewqkohrwpdvnkurvydvmihvffcoukyuybgpnevakkfzybghgrcrqilycmdikrjkpgeybocsvnokrvqvvrdlitwmukmfcazayyyklkwuvldjgfzinqkiwdpxfpwddpfdmscunbvygypdlkfgwubsnplrdkpxeiukgiffjqnhgrlruifyjqdhfpwqwiypwbkqwpurunnbcmdikflepxebysgmnybonenwwswgmjmihhdnbqbndwukkiwbvikvtybsnxdyzqnomiybuihieykhlecrqamilifkwxybgvjpvldlnqwvdhhrwbcixrckrhnrcocpivtyqglbebiymiwoculwccpxenvlphjqdruijqiqiojewmroldljbgfypyijlebowomiwoculwcoqidvjvdhmrjruqtlbrrxfkycdnlfcruimeoqwvnqkqbndoubgogfcruvdqwschgrbqpvmnpruierjfroglwbdvdburvgflufrxzteddhgdlazaxdlocpkeujdgfyygrxzwwknhgdlazawrwjrxmeoruydvemdxjvilkhddlafkwjeyzmldznkqjwzudxjwzruqfralznjswnrtluubknlkykklnswmrhgvcbzmfvjqiywnlqzbtbaihleawocawljojgdvclzomiwmuqinlenhgrsinhifhqnhgrziculbvruivbyakqpryvrveflruigdljrohnjruhlqubknlaokudtyukpyjaudgkwuyxdkmiwdrxmiwvhogfcmzvmisiqimiybkiwaudgonqvldnjqdazaybwqlgwlyxkiyybokbldvldvnbzsaihfvlbgwlwjailylovgmfcnrblfvkdlsybqqijewiclvyaidlltwbkogrjqmijvvapxeyjyknqryykynqvldnldjrnqswefdvfdljkvtybschgrydfodovldhnwzqqodovldodfzeqijyrqpamjkowhtewkfiqvvomijvvanhnwzeqijywdavlrcudiarlxqqpfvkdlsawohhvbbscifajsxnmrjschgrbqpvmnplrehienzxzbpiqgmybocgwybqdylbexugppbinilburrketuddnntalzvlswoiogfcurxeyeudggnliqnntalzawswsiogfcjqijtcvhhhimofgfimocplswbplnyvndkfiyudpqrpiqigfsmuqfrjfdoprvldunovqgmlewicwlkjihpnqcqqtnqipqgwxwkcqhybqvwiduuuqwnjscolehscukdopdvfybqpxzrzklxdpvlphmneupxvkjojhnxynfiwryrknlfjvqijuasknmiwkbijyexknlujqpelecvqqhpurrodovqckpdcgrbvnoczaiuvqpvnymihmdvzjagwuwsknleyedxnvcsqvnyyrdpdekndtlelqnouvieigwlvldawuwdnhjqdscujyvdrdtywkkqprobgiybvocpnqiocpmiwjhliuonixlbcsknnqgruivdjqmqmijsxnmnlnvhgncqbgmicqjvlycschgruduijevkjqtwdjrtnqwruifrkddhfflihvgrydkogralzmdvzjnnjewazaykzqpotewvhhwnvazaykyscogdzniqfrvldsljvizxlnpruifrhqcujywkzbkdjoggfrmqnhgrjqrojqudekwdbskgfflndkeflevqtecldikyeoxvlrlppomvjqpxeflphhmflevqteklrleyekiilkybggwpjskgwlvldljbvnrxlnpazaykeqfmlxbizolnodoqvbybgqteciqvdpcnzxzawxzvlpwqyjleuqcwlybqfojulqnonbrykkhdznmimpwqchhnioqplqcmuiwruruiyjeyqzdjedvqteciqvdprqjqprceqijyvldmdezjmixnsqnopdzngiffjqrogdzxzbifpqrpnopqqiwxwsnnjwpiapldvlknlaurkiyrcrknnqiscqtevigkvbciqvdpukknltwuzvvnpihvvrcrdvedmkoqvybqvojjvifivnouhomqwqgoxieiniqrvmdiwybqwlldcyqifnprugfpedipjqdruikrycdqsybqcioyaiqledljrojjviknltulptlxbiniwaeruhgrdqigzivkzbmiukbqywdocpmiwpdkxrexknlqwtkbdeugcqhfluvnldjrknjyvldotkjqfiknwrbvdywvhhdqwpzipdljrhfxybnjlepqjhijybggmdzkzvgjsqnjlepqjhijporhgfcocqjbukrxmiwldkyyalrwgpunixlswdmiyrycuieamruixdjoekwnprugwzubxmgrlazayrycuydvjldgzivazafiyniplbudddtyebiysnjjdonewocpvnokukiwbyculepiqntqiqqkwumihogdznknnecraqyljqphlevlrvfyuxvqtewfdkijeyqolxjqkomnvldmnqdazafieyipwnvvikprvldmnqdxzvyrhqplnqiruipyeruimewqnhgrpnzmleciaokeubxkyraschlecjqijtcddljywjphmiwvqijzponhmdrndqsybqpxzrzknknuyklawzviphtawdzolbwquqhbasahijudhxhiundydvkocxdyaoiswnjqeiwxjqdjfdujknlyovdvdbwrzhgrcghxbnbuzomqeviifpuxkvtqlqqjirykdvtqcmrbmwmrhvmwwkjkwywniedewomqtyjippfybocnjewknhydledhgdvcqijyoddohfvlzamayclddqwkukarvldnjedqnhfiwniomiwuzomyynlkmfhqromiwndkfyubkiiwuedxmdljknlewsnnjednvkefpxdvlqkqmimpwqckwnjokqydljpxjvkrrqwrwdmizeyrdbtwvlphvnojzxdyboeimnzseienabknlewbzmwnpoakmiwdcqyybqbijwvlzbjqobjllaorpddswoilqridphloonknjylizxlpuninjswrzlnswjzmwruruiyjeyqvlqemcqyjeyqmldzruqwwmmuiwdnyxuirjurofrccphxiubxnnbroilenwkuijkxqplmnsqknlrlfrqtbxdpgfrcudawzlibgwlzaiqwlaqqivnoogvldsscydvjuzhgrjknllrxocpmiwbnnlpegdhdlufdydvrsqhgybqxiytexknleycdgfflazayteruiybzicunqiuvbjybqqkwusiknledqngyrdojnnwdocpmiwamiznvudkwuumpxmrdofqmiwdpxedpoknleybggqriikxnlbrpxeybqnijbeudqsnodjnnwdddxjewihvuvcrrbnxyrrqwbybgodtwoqiqvvihvyriddhfpbqcxnlbrjqprcocpvnorzqjewjpvbwuqgqhqybgdluydlmnybobgiwybgmgrluzvwflejqprcocpvnooqifyunipjegkkkwuoppxebyakqmiwjpyhfvlpmnwzspefyunipjegskgfbvywgeyepikvdjiiihfvlknlqueuhjqdruiedmruivpeyipqnvliktlbokydvvldedvlrpgwswsiiefluromfcbzhjiunikwnygkvlrubknleyscgfqerpmlrxscuhfznzmqrbiipgrjqrojkydppdmvldplrxocpgfilpvlqwoqiyyeicijqeruiyybochgrssgllswnkqlfvldvhiwbromnejpwirydfgyeedmisnjqvqtjeyxkcrdschdtwocpfdaazayfsoximiwbvqtbysgginhqvqtaorrxmeoruydvzieiejeyqolwpscelpbqcydvwboqvwefrxzjeyqxlfilmqyfvcdkfrcrzdldhsqhtrzieihiucugfqerplhdmknjyflerxzfcoimjjcjvgwlmihwjqliknjswazamiybghgrgbzmirdedqsfvokhgrcofimfsqaqyjeyknnbvizdtbmnrtnqirzswnaocpbqemiielwsnhdnrynyfrwgrxzfvkdlsyenrtljeyfkvburphvnodbgwuembkmxbscumiwppofrjkmyjqdmphxiubxydvsovolrybhxhdzgrxzyempvejeyqvnlbrukwuybgkkeekkgmvvqkqhdjjvqtezqahgdljpxejeyfkvbyarxvnodrxwnkqcwliemcqqwwsnhgrebdkwubibgzqeviinbvldqmiwdmambbihlejeyjldbwazayrmqnkwuzsnhlqymugirmihmdvzjuijeyfzgxralrokrjscunqvldimiwdzxlbwqloprubwvjjwdpxeybqzhgrjscjjflocpnqvldokfjskqsrycuhgrjqrojaemdvsnjuvokfjskqwxwqeiyjbycpyrdadkybnqnafnpbprjewruelrvkoifvciahgrklqgfyuocgwdioqplqyuzxzybqugiwciallaybzxjqdruivyynlldqiocpldklkgprnqnafnpbprjewruudrcobkvbyarxzyezdotbexknlxbdromfybfyseuqcpnowoqmlbboilwrhqqxlswdpuyrwupyzndxdieybqztleyvhxedlrpuyryrfkwiykkmdiwoqhfnlqmllrdkpxeybqzhgrjxzvqrydnognongqwrvqiljwuqbnnxbjzifqeruayymihxdeybvqwrwnnihimbzhfdmscydvjldkyyvlphmiwlzafrexugfoyckonbvizopdznaqyiukakwxuqnkwubqukeyendkaruraqywydxiybxojiqrbscplswdvwincqgpdnjsnkpjcrdvvbwoiiepuruolswbnijwcmpgmfleromiwlzqsbexkgpralphnovdzaqwwkuqtwdvdkwramrxenaschgrwonhlelmplinpazayieynivnoupysnjedhmiwicihfvlbndtmihnjswnpaziwjmamqwfdvmiwicihfvlbndtmihnjswmdjmybqqipvcrmifnsqknnqikkvjqiqiyfdkddpnqcoihnyukrxdvjrdkybybggwybqnijnodxqefllrozeycrqtbvlrvfyasileeublafdznknluwmgvdkybghgrvqpvvnooqiqvvoavjlsqchdomihvzfybkolwpofqtybrukmbwqloqewogkwuyvigwubocpmiyruqiucruixvxxzvjybsqomjsihhgfpazahnongvnbwvhhjxovrhjaefdvjxwocpxnobkvvdljniiomihmdvzjrxerwjmixnsqxqewugdgsfaqqivnosbqtwdbzhsfljaktwvmrhgybqnijdvnzmmfdqrhnbyezqebbswkwueyqwjkvorxnbyviinyukzxijmihvfyeupwgybokgffljrodedqqognongydvcskaknlojldvdazahnongxdycqdhgrrihxedjaigwrrqkmlrlicixnobkvvdljpxdybqqxdevldddvljpvvbviciqrvmdiwdpoqejqdoakyturrojkurvydvkocxdycskaknlojldvdkdtlqkqchteuqnkzncqeiwpbskienhqnvdbwxqqpddqdjadzndyswmscumnvldownamugmrcyfenyexknlteychjflicidovldolswbfiwpbibkmxbqghgrpnrugycorpnbwqpdidkgnjdyebknlpubxqsybqniarlrupdswrzpjjvldjlnxndgwyboktjwzqvhlwziaolswbmljxgjztlbalzbirarzhgrcyfenyexknlblibypnobkknqubknldorhewfioknlewjplitmkzvynakpxeaodrieybqfgwtmepverlocphiwbpjyfzddhtelqgkwucpqgwlkofimnaqghgrwoqhgybqqizewmrxpjioqplqrqpamfpyibinaqqotqzslijwziknlepnzmlecocppjlqrugaednwjtwrzdlienghgrsocpmiwaplibysghdtwmuiwdorhewxeudojlysckmbwqggwlvsfihfznvqtqerxgarokzbmiwkdiebexknlbwxiqhrjkknjyaqfkviyfdhgrsscqteioqplqcskgffljdietukdvvfpsnhyrvcukwrspkygdljkqprlocpyrkqrtlqerugwlrykgmfclzjlwwknxlbcsagfyjqkwgdpyilgdljpxeoubgxdqwrzvlxwseinwebxbdewrdvwfvamixdokdhgrjqrogdznfilysahxheurkiwkeqfojqduvawkyschluxsjhtewkpvmfconhlkpdzewdvyqimnaoqpmiwscbnqurdkhnjgzbjevsnkpfcrjkyswjrxmnybrejlwqeiwybqukwucrukmtygdwynabnqsybiqxfdjqmimywdknjqujiigdljnqtesinhfdkddpmrydnxlswdnilzeyqivrcqeiyjsocgfybqgifxwbgkwyexdtlemgrxzdljdtlemkikarvlphlswdigardsahgriddkmljocpsdvldvdonqnafiyjlxdplmukmpykugeuwbbgmiubugppeyipgrliknjswkkqduubpmlnplrefrzxbkfybqiqarexoaedcuzhgrjianlecicllbcrukwybqiqarexfkyjpiqzlbokknlewoqimijqdeneyciifnpihvqeeruiycwkhownvadhyrkiqpluubknlaeilhgrpsqomyboknlpykpejqzslivnoocpprvldolxebghgdvldnjuykdxfrexuapnodpxeybqknnedrukmiwgcihiwmpojxebtaleedkndviljqwhoqqiexjyjgsfwjzxljeypvlxjyjgsfwjhjdqsauijevocpmiwbpgibvlphkfwdjivnodukwucpriyxwruihdznnqstmldkyyybghdtedqqhpbqckfyjoculexonolbraknnbiiiudybouihfzncqmzlibhgdvrbqqwwjuiyrbqbgiwdqdenyvlddinejzbdqwupxvnoupygdhquijediahgrrndofrduzawyyscgmfcruigfildomteychjflscqteaiqlebbihlejeyqijxbruifvsurhvnomzaiuboeidqzazxluwkrvldljknjyvigifxwbgkwurqbgmivlzolpbigmlwzschgrdqdjlbvfplirmrukmfcmuynyukjkiwwjknlazqnolusihxmdubdtlemruqtlbrrnjswsfjyfcicieflqyjyrckrqwfsynhsewqmypjdqdpfozoxgfiwniqoqocpudndnhwb"
p=list("****")
for i in range(26):
    p[0] = chr(ord('a') + i)
    for j in range(26):
        p[1] = chr(ord('a') + j)
        for k in range(26):
            p[2] = chr(ord('a') + k)
            for l in range(26):
                p[3] = chr(ord('a') + l)
                if (s.count("".join(p)) >= 20): #这里的20是可以调的，得到合适数量的四位字符串即可
                    print("".join(p)) #到此得到了几个在密文中重复了20次以上的串

#接下来选其一把它们在明文中的位置记录下来
def find_sub_n_index(str,substr,time):#自己写的算法，返回子字符串第n次出现时的下标
    begin=0
    while(str[begin:].find(substr)!=-1 and time>0):
        begin+=str[begin:].index(substr)+4#这里的4是因为选的子字符串长度为4
        time-=1
    return begin-4
position=[]
key="erui"
for i in range(1,20):
    site = find_sub_n_index(s, key, i)
    position.append(site)
get_gcd=[]#开始求间距的最小公倍数
for i in range(18):
    get_gcd.append(position[i+1]-position[i])
for i in range(2,min(get_gcd)):
    flag=1
    for j in range(18):
        if(get_gcd[j]%i!=0):
            flag=0
            break
        if(flag):
            gcd=i
print("一轮长度：",gcd)#一轮密钥长度为6


一轮的长度实际上是两个密钥长度的最大公倍数，但我们还是不知道具体两个密钥有多长，不过没关系，直接当6处理，其中重复的求出来了自然就知道有多长了

爆破密钥

首先需要一些关于英语词频的常数：大量英文中每个字母出现的频率是有统计意义上的平均值的，一篇单词数足够的文章，其重合指数接近0.065（重合指数的定义请问度娘），那么解密出来的明文应该是符合这个常数的。但是明文是由不同的6个不同密钥加密的，为了算法上好实现，建议先将原密文分成6组，分别解密后算重合指数，重合指数最靠近0.065的大概率就是真正的密钥。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
best_index=0.065
dic_index={'a': 0.08167,'b': 0.01492,'c': 0.02782,'d':0.04253,'e': 0.12702,'f':0.02228,'g': 0.02015,'h':0.06094,'i':0.06966,'j':0.00153,'k':0.00772,'l':0.04025,'m':0.02406,'n':0.06749,'o':0.07507,'p':0.01929,'q':0.00095,'r':0.05987,'s':0.06327,'t':0.09056,'u':0.02758,'v':0.00978,'w':0.02360,'x':0.00150,'y':0.01974,'z':0.00074}
s=
import gmpy2
import math
def index_of_conincidence(c,i,j):#解密➕算重合指数
    fre=[0]*26
    sum=0
    for k in c:#解密➕算频率
        if(ord(k)-ord('a')-j>=0):
            k=chr(gmpy2.invert(i,26)*(ord(k)-ord('a')-j)%26+97)#模运算求逆就要用到逆元了
        else:
            k=chr(gmpy2.invert(i,26)*(ord(k)-ord('a')-j+26)%26+97)
        fre[ord(k)-ord('a')]+=1
    for k in range(26):
        sum+=(fre[k]/len(c))*dic_index[chr(ord('a')+k)]#这里和一般计算重合指数的方法不太相同，但实际上道理上是一样的。
    return sum
def find_key(c):
    index=1
    for i in range(26):#爆破乘数
        if(i%13==0 or i%2==0):#有相同因子的求不出逆元，解密后明文不唯一，必须舍弃
            continue
        for j in range(26):#爆破加数
             if(math.fabs(index_of_conincidence(c,i,j)-best_index)<index):#谁最接近0.065？
                 index=math.fabs(index_of_conincidence(c,i,j)-best_index)
                 key1=i
                 key2=j
    return (key1,key2)
t=[]
key3=[0]*6
key4=[0]*6
for i in range(6):#还原密钥
    temp="".join(["".join(s[cycle*6+i]) for cycle in range(len(s)//6)])
    t.append(temp)
    key3[i]=find_key(temp)[0]
    key4[i]=find_key(temp)[1]
for k in range(len(s)):#解密
        if(ord(s[k])-ord('a')-key4[k%6]>=0):
            k=chr(gmpy2.invert(key3[k%6],26)*(ord(s[k])-ord('a')-key4[k%6])%26+97)
        else:
            k=chr(gmpy2.invert(key3[k%6],26)*(ord(s[k])-ord('a')-key4[k%6]+26)%26+97)
        print(k,end="")

[AFCTF2018]Tiny LFSR（python3的类型转换）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import sys
from binascii import unhexlify

if(len(sys.argv)<4):
	print("Usage: python Encrypt.py keyfile plaintext ciphername")
	exit(1)

def lfsr(R, mask):
	output = (R << 1) & 0xffffffffffffffff
	i=(R&mask)&0xffffffffffffffff
	lastbit=0
	while i!=0:
		lastbit^=(i&1)
		i=i>>1
	output^=lastbit
	return (output,lastbit)

R = 0
key = ""
with open(sys.argv[1],"r") as f:
	key = f.read()
	R = int(key,16)
	f.close
	
mask = 0b1101100000000000000000000000000000000000000000000000000000000000

a = ''.join([chr(int(b, 16)) for b in [key[i:i+2] for i in range(0, len(key), 2)]])

f=open(sys.argv[2],"r")
ff = open(sys.argv[3],"wb")
s = f.read()
f.close()
lent = len(s)

for i in range(0, len(a)):
	ff.write((ord(s[i])^ord(a[i])).to_bytes(1, byteorder='big'))

for i in range(len(a), lent):
	tmp=0
	for j in range(8):
		(R,out)=lfsr(R,mask)
		tmp=(tmp << 1)^out
	ff.write((tmp^ord(s[i])).to_bytes(1, byteorder='big'))
ff.close()

1
2
3
4
python Encrypt.py key.txt Plain.txt cipher.txt
python Encrypt.py key.txt flag.txt flag_encode.txt
rm flag.txt
rm key.txt

通过已知信息，我们发现cipher.txt和flag_encode.txt都是由同一个key.txt和另一个文件异或而来

所以，关键是求出密钥

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
mask = 0b1101100000000000000000000000000000000000000000000000000000000000

a = ''.join([chr(int(b, 16)) for b in [key[i:i+2] for i in range(0, len(key), 2)]])

f=open(sys.argv[2],"r")
ff = open(sys.argv[3],"wb")
s = f.read()
f.close()
lent = len(s)

for i in range(0, len(a)):
	ff.write((ord(s[i])^ord(a[i])).to_bytes(1, byteorder='big'))

for i in range(len(a), lent):
	tmp=0
	for j in range(8):
		(R,out)=lfsr(R,mask)
		tmp=(tmp << 1)^out
	ff.write((tmp^ord(s[i])).to_bytes(1, byteorder='big'))
ff.close()

由上面那串代码我们可以发现，key的值与plain.txt的前几个字符进行了异或，那我们将cipher.txt与plain.txt异或，那它前几个字符不就是key的值了嘛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import re
from Crypto.Util.number import*

#指定文件在相对路径
import os, sys
os.chdir(sys.path[0])

cip = open('cipher.txt', 'rb').read()
plain = open('Plain.txt', 'rb').read()
cip = bytes_to_long(cip)
plain = bytes_to_long(plain)
key = hex(cip^plain)[2:]
print(key)

s = re.findall(r'.{16}',key[::-1])
print(s)

image-20250312221945673

我们发现前16为缺了一位数据，应该补0，即密钥为”0123456789abcdef”

由mask可知，密钥应该为16位16进制数据，即64bit，与mask长度一致。

那为什么是前面补0

image-20250312222606370

我觉得很合理(赞同),int类型是4位，long类型是8位，因此异或后应该也是208位，但实际上去掉0x，异或后只有207位，所以我们需要在前补0

由于对flag的加密仅仅只用到了异或，而未进行其它加密，所以当我们有了key之后，只需再次与密文继续异或就能得到flag了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import os,sys
os.chdir(sys.path[0])

key = '0123456789abcdef'
R = int(key,16)
mask = 0b1101100000000000000000000000000000000000000000000000000000000000

def lfsr(R, mask):
	output = (R << 1) & 0xffffffffffffffff
	i=(R&mask)&0xffffffffffffffff
	lastbit=0
	while i!=0:
		lastbit^=(i&1)
		i=i>>1
	output^=lastbit
	return (output,lastbit)

cipher = open('flag_encode.txt','rb').read()
a = ''.join([chr(int(b, 16)) for b in [key[i:i+2] for i in range(0, len(key), 2)]])
ans = []
lent = len(cipher)

for i in range(0, len(a)):
	ans.append(chr(cipher[i]^ord(a[i])))

for i in range(len(a), lent):
	tmp = 0
	for j in range(8):
		(R,out)=lfsr(R,mask)
		tmp=(tmp << 1)^out
	ans.append(chr(tmp ^ cipher[i]))

flag = ''.join(ans)
print(flag)

老文盲了（汉字拼音）

打开页面

发现内容为

1
罼雧締眔擴灝淛匶襫黼瀬鎶軄鶛驕鳓哵眔鞹鰝

不知道是啥加密方式，我们转拼音看看在线汉字转拼音

1
bì jí dì dà kuò hào zhè jiù shì fǔ lài gē zhí jiē jiāo lè bā dà kuò hào

6，flag出了

1
flag{淛匶襫黼瀬鎶軄鶛驕鳓哵}

LeftOrRight（二叉树）

image-20250313200511546

image-20250313200524996

我们在图片中找到了两串hex字符串

提示提到

1
Left?Middle?No，I want right！（flag is right？！）

这里讲的一个是二叉树的前序、中序和后序，我们已知了前序和中序，要求后序

我们去网上找一个求后序的脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# f09e54c1bad2x38mvyg7wzlsuhkijnop
# 905e4c1fax328mdyvg7wbsuhklijznop

def fromFMtoL(mid):
    global las  # 全局后序遍历
    global fir  # 先序遍历
    root = fir[0]  # 取出当前树根
    fir = fir[1:]  # 取出树根后 先序遍历把根拿出来 下面一个元素做树根
    root_po = mid.find(root)  # 在中序遍历当中树根的位置
    left = mid[0:root_po]  # 左子树
    right = mid[root_po + 1:len(mid)]  # 右子树
    '''
    后序遍历： 左 右 根 
    先左子树 再右子树 最后跟
    '''
    # 有左子树的时候
    if len(left) > 0:
        fromFMtoL(left)
    # 有右子树的时候
    if len(right) > 0:
        fromFMtoL(right)
    # 树根写进结果
    las += root


if __name__ == "__main__":
    # fir = input("请输入先序遍历：")   #前序遍历的结果
    # mid = input("请输入中序遍历：")   #中序遍历的结果
    fir = "f09e54c1bad2x38mvyg7wzlsuhkijnop"
    mid = "905e4c1fax328mdyvg7wbsuhklijznop"
    # fir = "ABC"
    # mid = "BAC"
    las = ""
    fromFMtoL(mid)
    print(las)
   
#951c4e03xm82yw7gvdakhusjilponzbf

[GKCTF2020]小学生的密码学（仿射变换）

1
2
3
4
5
e(x)=11x+6(mod26)

密文：welcylk

（flag为base64形式）

这种形式的加密手法是仿射变换，其加解密分别是

image-20250318171748271

由题目可得，a=11，b=6，我们需要做的工作是根据密文c，密钥a/b得到明文m，这里a^-1^是 a在模 26 下的乘法逆元我们用invert进行计算

注意仿射变换26个字母按数字0~25记，因此在需要将密文ASCII对应的数值减去97，解密完恢复成字母即加上97

此外，题目要求最后的flag为base64形式，因此还需借助Python的base64库中b64encode函数。需要注意的是在Python3中，字符都为unicode编码，而b64encode函数的参数为byte类型，所以必须先转码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from gmpy2 import invert
from base64 import b64encode

c = "welcylk"
a = 11
b = 6
n = 26

in_a = invert(a, n)
print(in_a)
# in_a = 19

m = []
for i in c:
    modified_c = ord(i)-97
    m.append((modified_c-b)*in_a % 26)
flag = ""
for mi in m:
    flag += chr(mi+97)
print(b64encode(flag.encode()))