crypto rsa

RSA加密算法

rsa基本组成

在RSA加密算法中，以下是常用的符号和对应的含义：

e：公钥指数（exponent），用于加密操作。通常为一个较小的固定值，例如65537。

p和q：两个不同的大素数，用于生成RSA密钥对。它们的乘积n (n = p * q) 是模数（modulus），用于加密和解密操作。

d：私钥指数（exponent），用于解密操作。它通过使用扩展欧几里得算法计算得到，满足 e * d ≡ 1 (mod φ(n))，其中 φ(n) 是欧拉函数值。

n：模数（modulus），也是公钥和私钥共享的一个参数。它是两个素数 p 和 q 的乘积，即 n = p * q。

φ(n)即phi：欧拉函数（Euler’s totient function）的值，表示与 n 互质的正整数的数量。对于两个素数 p 和 q 的乘积 n，φ(n) = (p-1)*(q-1)。

m：明文（plaintext），需要被加密的消息或数据。m=c^d mod n

c: 密文，c=m^e mod n

总结：
e是公钥指数，p和q是素数，d是私钥指数，n是模数，phi是欧拉函数值，m是明文。

已知p,q,e求d（rsa）

我们导入python的gmpy2库，这个库求rsa超好用

from gmpy2 import invert
p=473398607161
q=4511491
e=17
phi=(p-1)*(q-1)
d=invert(e,phi)
print(d)
#flag{125631357777427553}

成功得到flag

已知p,q,e,c 求明文m [buu rsarsa题]

from libnum import n2s,s2n
from gmpy2 import *
p =9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q =11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e =65537
phi=(p-1)*(q-1)
n=p*q
c =83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
d=invert(e,phi)
m=pow(c,d,n)
print((int(m)))
#flag{5577446633554466577768879988}

已知p,q,dp,dq,c 求明文m [buu RSA1题]

http://t.csdnimg.cn/KOuWf

小记一下：在RSA密码中，dp和dq是私钥的参数，用于加速中国剩余定理（Chinese Remainder Theorem, CRT）解密算法。

dp：是d对p-1的模反元素（modular inverse）。即 dp = d mod (p-1)。

dq：是d对q-1的模反元素。即 dq = d mod (q-1)。

这两个参数在CRT解密算法中起到加速解密过程的作用，通过使用CRT算法可以减少模幂运算的计算量，提高解密效率。具体来说，当进行解密时，先对密文进行两次模幂运算，分别使用dp和dq，并分别取得结果m1和m2。然后根据CRT算法，使用p、q、dp、dq以及模数n计算出明文m。这种方式相比于直接使用d进行模幂运算，能够大大提高解密速度。

m = (m1 + (I * (m2 - m1)) * p) % n

from libnum import n2s,s2n
from gmpy2 import *
p=8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q=12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp=6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq=783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c=24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
I=invert(p,q) //求p和q的逆元
n=p*q
m1=pow(c,dp,p)
m2=pow(c,dq,q)
m = (m1 + (I * (m2 - m1)) * p) % n    #求明文公式
print(n2s(int(m)))
#noxCTF{W31c0m3_70_Ch1n470wn}——>flag{W31c0m3_70_Ch1n470wn}

逆元

给定整数 𝑎a 和模数 𝑚m，如果存在一个整数 𝑥x，使得：

𝑎⋅𝑥≡1(mod𝑚)a⋅x≡1(modm)

那么这个 𝑥x 就是 𝑎a 的模 𝑚m 下的乘法逆元，记作 𝑎−1(mod 𝑚)a−1(mod m)。

已知e1,e2,c1,c2,n 求明文m(共模攻击）[buu RSA3]

小记一下：

根据给定的参数 e1、e2、c1、c2 和模数 n，下面是求解明文 m 的一般步骤：

使用扩展欧几里得算法计算 e1 和 e2 的最大公约数 gcd(e1, e2)。确保它等于 1，否则无法进行共模攻击。

计算 e1 在模 e2 下的模反元素 s1 = e1^-1 mod e2，以及 e2 在模 e1 下的模反元素 s2 = e2^-1 mod e1。

计算明文 m：

计算 x = (c1^s1 * c2^s2) mod n。
计算 m = x mod n。
需要注意的是，在实际计算过程中，可以使用模幂运算算法和模反元素算法来进行计算。

此外，如果 m 不在 0 到 n-1 的范围内，还需要对结果进行适当的调整，以保证明文 m 在正确的范围内。

from gmpy2 import *
c1 = 22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n = 22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1 = 11187289
c2 = 18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2 = 9647291
# 扩展欧几里得算法
# return (r,s1,s2) 其中，r为e1和e2的最大公约数，s1 s2满足e1*s1 + e2*s2 = 1
r,s1, s2 = gcdext(e1, e2)  # 计算s1，s2,此处r=1,符合共模攻击
m = (powmod(c1, s1, n) * powmod(c2, s2, n)) % n  # 计算明文m
m = hex(m)[2:] # 例如 "0x1f",通过切片操作 [2:]，我们去掉了前两个字符，即 "0x"，只保留了后面的部分，例如 "1f"。
print(bytes.fromhex(m).decode())
#flag{49d91077a1abcb14f1a9d546c80be9ef}

已知e,n,dp,c 求明文m（dp泄露）[buu RSA2题]

小记一下:

dp=d%(p-1)

dq=d%(q-1)

dp*e = i*(p-1)+1

from gmpy2 import *
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657

c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

for i in range(1, e):  # 在范围(1,e)之间进行遍历
    if (dp * e - 1) % i == 0:
        if n % (((dp * e - 1) // i) + 1) == 0:  # 存在p，使得n能被p整除
            p = ((dp * e - 1) // i) + 1
            q = n // (((dp * e - 1) // i) + 1)
            phi = (q - 1) * (p - 1)  # 欧拉定理
            d =invert(e, phi)  # 求模逆
            m = pow(c, d, n)  # 快速求幂取模运算
m=hex(m)[2:]
print(bytes.fromhex(m).decode())

#flag{wow_leaking_dp_breaks_rsa?_98924743502}

已知p,q,e,n,文件加密密文求密文m [buu RSA题]

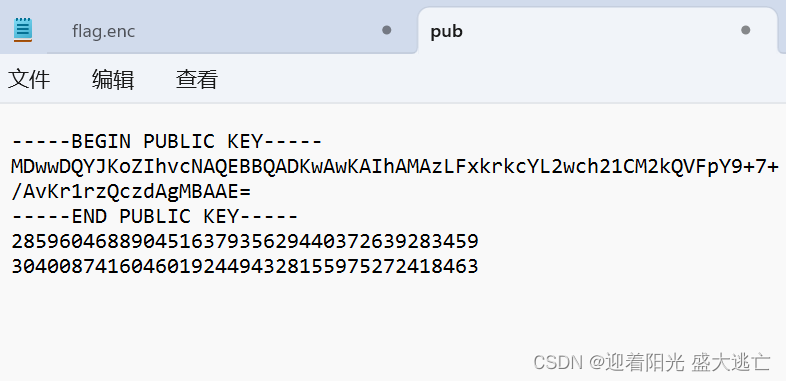
在这里插入图片描述

公钥解析后得到e和n，分解质因数得到p,q，顺势得到d

e= 65537

n=86934482296048119190666062003494800588905656017203025617216654058378322103517

p= 285960468890451637935629440372639283459

q= 304008741604601924494328155975272418463

d=81176168860169991027846870170527607562179635470395365333547868786951080991441
enc文件不能直接读，应该用代码读

from Crypto.Util.number import bytes_to_long
with open("C:\\Users\\11\\Downloads\\0eaf8d6c-3fe5-4549-9e81-94ac42535e7b\\flag.enc","rb") as f:  #以二进制读模式，读取密文
    f = f.read()
    print(bytes_to_long(f))
    #c=29666689760194689065394649908301285751747553295673979512822807815563732622178
from Crypto.Util.number import bytes_to_long
from libnum import n2s
e= 65537
n=86934482296048119190666062003494800588905656017203025617216654058378322103517
p= 285960468890451637935629440372639283459
q= 304008741604601924494328155975272418463
d=81176168860169991027846870170527607562179635470395365333547868786951080991441
c=29666689760194689065394649908301285751747553295673979512822807815563732622178
m=pow(c,d,n)
print(n2s(m))
//b'\x02\x9d {zR\x1e\x08\xe4\xe6\x18\x06\x00flag{decrypt_256}\n'

已知p+q，(p+1)*(q+1),c,d求明文m（[GUET-CTF2019]BabyRSA ）

(p+1)(q+1)=pq+1+p+q

n=p*q

m=c^d mod n

写个脚本

from libnum import n2s
a=0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
b= 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e =0xe6b1bee47bd63f615c7d0a43c529d219
d =0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
c =0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a

n=b-1-a

flag=pow(c,d,n)
print(n2s(flag))

//b'flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}'

Dangerous RSA（低加密指数攻击）

sa 的加密为 c = m ^ e mod n

当e 很小，n很大时，有两种情况

m ^ e 有可能小于 n 。此时， c = m ^ e 。密文 m = c 开e次方
当 m ^ e > n 。此时。 m ^ e = kn + c 。 k 是整数。对 k 进行爆破，就能找到对应的m

#python3
## -*- coding: utf-8 -*-#
from gmpy2 import iroot
import libnum
e = 0x3
n = 0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
c = 0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
 
k = 0
while 1:
    res = iroot(c+k*n,e)  #c+k*n 开3次方根 能开3次方即可
    #print(res)
    #res = (mpz(13040004482819713819817340524563023159919305047824600478799740488797710355579494486728991357), True)
    if(res[1] == True):
        print(libnum.n2s(int(res[0]))) #转为字符串
        break
    k=k+1
    
#b'flag{25df8caf006ee5db94d48144c33b2c3b}'

iroot(c+k*n,e)为c+k*n开e次方

mpz用来处理大整数和需要高精度运算

RSAROLL（rsa）

题目信息没看懂，找大佬的wp才知道{920139713,19}，一个是n，一个是e，后面那一大串是拆分的c

我们通过网站分解n得到

p= 18443

q=49891

所以已知信息有

p= 18443

q=49891

n=920139713

e=19

我们写脚本来爆c

import libnum
from Crypto.Util.number import long_to_bytes
from gmpy2 import *
list1 = [704796792,
         752211152,
         274704164,
         18414022,
         368270835,
         483295235,
         263072905,
         459788476,
         483295235,
         459788476,
         663551792,
         475206804,
         459788476,
         428313374,
         475206804,
         459788476,
         425392137,
         704796792,
         458265677,
         341524652,
         483295235,
         534149509,
         425392137,
         428313374,
         425392137,
         341524652,
         458265677,
         263072905,
         483295235,
         828509797,
         341524652,
         425392137,
         475206804,
         428313374,
         483295235,
         475206804,
         459788476,
         306220148]
flag = ""
n = 920139713
p = 49891
q = 18443
e = 19

for i in list1:
    c = i
    d = invert(e, (p - 1) * (q - 1))
    m = pow(c, d, n)
    string = long_to_bytes(m)
    flag += string.decode()
print(flag)

得到flag

1	flag{13212je2ue28fy71w8u87y31r78eu1e2}

rsa2

源码长这样，我们需要将N分解为p和q

p=9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183

q=11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937

然后改一下代码

N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
p=9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183

q=11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937
import hashlib
from gmpy2 import invert

phi=(p-1)*(q-1)

d=hex(invert(e,phi)).encode('utf-8')

print(d)
flag = "flag{" + hashlib.md5(b'0x13b8f87d588e2aa4a27296cf2898f56ab4c8deb5a1222ec080e23afecaf7f975L').hexdigest() + "}"

print(flag)

根据原题处理d值并输出

这里就是按照原题给的计算式去处理d值，这里有个小坑，就是由于Python2和Python3有一点区别，在Python3中，hex(d)得到的值在输出形式上相比Python2少了一个末尾的L，再用这个值去做hash得到的md5值也就不同了。经实验发现，正确的结果可以用Python2直接得到，或在Python3中做hash时给参数末尾加上L。

rsa5（低加密指数广播攻击）

低加密指数广播攻击特点

加密指数e非常小
一份明文使用不同的模数n，相同的加密指数e进行多次加密
可以拿到每一份加密后的密文和对应的模数n、加密指数e

此题给出的e很小且不变，给出了不同的公钥(e,n)和对应的密文c，也就是用不同的公钥加密相同的明文m

解题思路：

不同的模数n中可能存在相同的p或者说q

求出不同n之间的最大公约数 gcd()

得到p或q 可得d

有私钥d就能得到明文

import gmpy2
import libnum

e = 65537

n0 = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c0 = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320

n1 = 20918819960648891349438263046954902210959146407860980742165930253781318759285692492511475263234242002509419079545644051755251311392635763412553499744506421566074721268822337321637265942226790343839856182100575539845358877493718334237585821263388181126545189723429262149630651289446553402190531135520836104217160268349688525168375213462570213612845898989694324269410202496871688649978370284661017399056903931840656757330859626183773396574056413017367606446540199973155630466239453637232936904063706551160650295031273385619470740593510267285957905801566362502262757750629162937373721291789527659531499435235261620309759
c1 = 15819636201971185538694880505120469332582151856714070824521803121848292387556864177196229718923770810072104155432038682511434979353089791861087415144087855679134383396897817458726543883093567600325204596156649305930352575274039425470836355002691145864435755333821133969266951545158052745938252574301327696822347115053614052423028835532509220641378760800693351542633860702225772638930501021571415907348128269681224178300248272689705308911282208685459668200507057183420662959113956077584781737983254788703048275698921427029884282557468334399677849962342196140864403989162117738206246183665814938783122909930082802031855

n2 = 25033254625906757272369609119214202033162128625171246436639570615263949157363273213121556825878737923265290579551873824374870957467163989542063489416636713654642486717219231225074115269684119428086352535471683359486248203644461465935500517901513233739152882943010177276545128308412934555830087776128355125932914846459470221102007666912211992310538890654396487111705385730502843589727289829692152177134753098649781412247065660637826282055169991824099110916576856188876975621376606634258927784025787142263367152947108720757222446686415627479703666031871635656314282727051189190889008763055811680040315277078928068816491
c2 = 4185308529416874005831230781014092407198451385955677399668501833902623478395669279404883990725184332709152443372583701076198786635291739356770857286702107156730020004358955622511061410661058982622055199736820808203841446796305284394651714430918690389486920560834672316158146453183789412140939029029324756035358081754426645160033262924330248675216108270980157049705488620263485129480952814764002865280019185127662449318324279383277766416258142275143923532168798413011028271543085249029048997452212503111742302302065401051458066585395360468447460658672952851643547193822775218387853623453638025492389122204507555908862

n3 = 21206968097314131007183427944486801953583151151443627943113736996776787181111063957960698092696800555044199156765677935373149598221184792286812213294617749834607696302116136745662816658117055427803315230042700695125718401646810484873064775005221089174056824724922160855810527236751389605017579545235876864998419873065217294820244730785120525126565815560229001887622837549118168081685183371092395128598125004730268910276024806808565802081366898904032509920453785997056150497645234925528883879419642189109649009132381586673390027614766605038951015853086721168018787523459264932165046816881682774229243688581614306480751
c3 = 4521038011044758441891128468467233088493885750850588985708519911154778090597136126150289041893454126674468141393472662337350361712212694867311622970440707727941113263832357173141775855227973742571088974593476302084111770625764222838366277559560887042948859892138551472680654517814916609279748365580610712259856677740518477086531592233107175470068291903607505799432931989663707477017904611426213770238397005743730386080031955694158466558475599751940245039167629126576784024482348452868313417471542956778285567779435940267140679906686531862467627238401003459101637191297209422470388121802536569761414457618258343550613

n4 = 22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067
c4 = 15406498580761780108625891878008526815145372096234083936681442225155097299264808624358826686906535594853622687379268969468433072388149786607395396424104318820879443743112358706546753935215756078345959375299650718555759698887852318017597503074317356745122514481807843745626429797861463012940172797612589031686718185390345389295851075279278516147076602270178540690147808314172798987497259330037810328523464851895621851859027823681655934104713689539848047163088666896473665500158179046196538210778897730209572708430067658411755959866033531700460551556380993982706171848970460224304996455600503982223448904878212849412357

n5 = 21574139855341432908474064784318462018475296809327285532337706940126942575349507668289214078026102682252713757703081553093108823214063791518482289846780197329821139507974763780260290309600884920811959842925540583967085670848765317877441480914852329276375776405689784571404635852204097622600656222714808541872252335877037561388406257181715278766652824786376262249274960467193961956690974853679795249158751078422296580367506219719738762159965958877806187461070689071290948181949561254144310776943334859775121650186245846031720507944987838489723127897223416802436021278671237227993686791944711422345000479751187704426369
c5 = 20366856150710305124583065375297661819795242238376485264951185336996083744604593418983336285185491197426018595031444652123288461491879021096028203694136683203441692987069563513026001861435722117985559909692670907347563594578265880806540396777223906955491026286843168637367593400342814725694366078337030937104035993569672959361347287894143027186846856772983058328919716702982222142848848117768499996617588305301483085428547267337070998767412540225911508196842253134355901263861121500650240296746702967594224401650220168780537141654489215019142122284308116284129004257364769474080721001708734051264841350424152506027932

n6 = 25360227412666612490102161131174584819240931803196448481224305250583841439581008528535930814167338381983764991296575637231916547647970573758269411168219302370541684789125112505021148506809643081950237623703181025696585998044695691322012183660424636496897073045557400768745943787342548267386564625462143150176113656264450210023925571945961405709276631990731602198104287528528055650050486159837612279600415259486306154947514005408907590083747758953115486124865486720633820559135063440942528031402951958557630833503775112010715604278114325528993771081233535247118481765852273252404963430792898948219539473312462979849137
c6 = 19892772524651452341027595619482734356243435671592398172680379981502759695784087900669089919987705675899945658648623800090272599154590123082189645021800958076861518397325439521139995652026377132368232502108620033400051346127757698623886142621793423225749240286511666556091787851683978017506983310073524398287279737680091787333547538239920607761080988243639547570818363788673249582783015475682109984715293163137324439862838574460108793714172603672477766831356411304446881998674779501188163600664488032943639694828698984739492200699684462748922883550002652913518229322945040819064133350314536378694523704793396169065179

n7 = 22726855244632356029159691753451822163331519237547639938779517751496498713174588935566576167329576494790219360727877166074136496129927296296996970048082870488804456564986667129388136556137013346228118981936899510687589585286517151323048293150257036847475424044378109168179412287889340596394755257704938006162677656581509375471102546261355748251869048003600520034656264521931808651038524134185732929570384705918563982065684145766427962502261522481994191989820110575981906998431553107525542001187655703534683231777988419268338249547641335718393312295800044734534761692799403469497954062897856299031257454735945867491191
c7 = 6040119795175856407541082360023532204614723858688636724822712717572759793960246341800308149739809871234313049629732934797569781053000686185666374833978403290525072598774001731350244744590772795701065129561898116576499984185920661271123665356132719193665474235596884239108030605882777868856122378222681140570519180321286976947154042272622411303981011302586225630859892731724640574658125478287115198406253847367979883768000812605395482952698689604477719478947595442185921480652637868335673233200662100621025061500895729605305665864693122952557361871523165300206070325660353095592778037767395360329231331322823610060006

n8 = 23297333791443053297363000786835336095252290818461950054542658327484507406594632785712767459958917943095522594228205423428207345128899745800927319147257669773812669542782839237744305180098276578841929496345963997512244219376701787616046235397139381894837435562662591060768476997333538748065294033141610502252325292801816812268934171361934399951548627267791401089703937389012586581080223313060159456238857080740699528666411303029934807011214953984169785844714159627792016926490955282697877141614638806397689306795328344778478692084754216753425842557818899467945102646776342655167655384224860504086083147841252232760941
c8 = 5418120301208378713115889465579964257871814114515046096090960159737859076829258516920361577853903925954198406843757303687557848302302200229295916902430205737843601806700738234756698575708612424928480440868739120075888681672062206529156566421276611107802917418993625029690627196813830326369874249777619239603300605876865967515719079797115910578653562787899019310139945904958024882417833736304894765433489476234575356755275147256577387022873348906900149634940747104513850154118106991137072643308620284663108283052245750945228995387803432128842152251549292698947407663643895853432650029352092018372834457054271102816934

n9 = 28873667904715682722987234293493200306976947898711255064125115933666968678742598858722431426218914462903521596341771131695619382266194233561677824357379805303885993804266436810606263022097900266975250431575654686915049693091467864820512767070713267708993899899011156106766178906700336111712803362113039613548672937053397875663144794018087017731949087794894903737682383916173267421403408140967713071026001874733487295007501068871044649170615709891451856792232315526696220161842742664778581287321318748202431466508948902745314372299799561625186955234673012098210919745879882268512656931714326782335211089576897310591491
c9 = 9919880463786836684987957979091527477471444996392375244075527841865509160181666543016317634963512437510324198702416322841377489417029572388474450075801462996825244657530286107428186354172836716502817609070590929769261932324275353289939302536440310628698349244872064005700644520223727670950787924296004296883032978941200883362653993351638545860207179022472492671256630427228461852668118035317021428675954874947015197745916918197725121122236369382741533983023462255913924692806249387449016629865823316402366017657844166919846683497851842388058283856219900535567427103603869955066193425501385255322097901531402103883869

n10 = 22324685947539653722499932469409607533065419157347813961958075689047690465266404384199483683908594787312445528159635527833904475801890381455653807265501217328757871352731293000303438205315816792663917579066674842307743845261771032363928568844669895768092515658328756229245837025261744260614860746997931503548788509983868038349720225305730985576293675269073709022350700836510054067641753713212999954307022524495885583361707378513742162566339010134354907863733205921845038918224463903789841881400814074587261720283879760122070901466517118265422863420376921536734845502100251460872499122236686832189549698020737176683019
c10 = 1491527050203294989882829248560395184804977277747126143103957219164624187528441047837351263580440686474767380464005540264627910126483129930668344095814547592115061057843470131498075060420395111008619027199037019925701236660166563068245683975787762804359520164701691690916482591026138582705558246869496162759780878437137960823000043988227303003876410503121370163303711603359430764539337597866862508451528158285103251810058741879687875218384160282506172706613359477657215420734816049393339593755489218588796607060261897905233453268671411610631047340459487937479511933450369462213795738933019001471803157607791738538467
 
n11 = 27646746423759020111007828653264027999257847645666129907789026054594393648800236117046769112762641778865620892443423100189619327585811384883515424918752749559627553637785037359639801125213256163008431942593727931931898199727552768626775618479833029101249692573716030706695702510982283555740851047022672485743432464647772882314215176114732257497240284164016914018689044557218920300262234652840632406067273375269301008409860193180822366735877288205783314326102263756503786736122321348320031950012144905869556204017430593656052867939493633163499580242224763404338807022510136217187779084917996171602737036564991036724299
c11 = 21991524128957260536043771284854920393105808126700128222125856775506885721971193109361315961129190814674647136464887087893990660894961612838205086401018885457667488911898654270235561980111174603323721280911197488286585269356849579263043456316319476495888696219344219866516861187654180509247881251251278919346267129904739277386289240394384575124331135655943513831009934023397457082184699737734388823763306805326430395849935770213817533387235486307008892410920611669932693018165569417445885810825749609388627231235840912644654685819620931663346297596334834498661789016450371769203650109994771872404185770230172934013971

n12 = 20545487405816928731738988374475012686827933709789784391855706835136270270933401203019329136937650878386117187776530639342572123237188053978622697282521473917978282830432161153221216194169879669541998840691383025487220850872075436064308499924958517979727954402965612196081404341651517326364041519250125036424822634354268773895465698920883439222996581226358595873993976604699830613932320720554130011671297944433515047180565484495191003887599891289037982010216357831078328159028953222056918189365840711588671093333013117454034313622855082795813122338562446223041211192277089225078324682108033843023903550172891959673551
c12 = 14227439188191029461250476692790539654619199888487319429114414557975376308688908028140817157205579804059783807641305577385724758530138514972962209062230576107406142402603484375626077345190883094097636019771377866339531511965136650567412363889183159616188449263752475328663245311059988337996047359263288837436305588848044572937759424466586870280512424336807064729894515840552404756879590698797046333336445465120445087587621743906624279621779634772378802959109714400516183718323267273824736540168545946444437586299214110424738159957388350785999348535171553569373088251552712391288365295267665691357719616011613628772175

n13 = 27359727711584277234897157724055852794019216845229798938655814269460046384353568138598567755392559653460949444557879120040796798142218939251844762461270251672399546774067275348291003962551964648742053215424620256999345448398805278592777049668281558312871773979931343097806878701114056030041506690476954254006592555275342579529625231194321357904668512121539514880704046969974898412095675082585315458267591016734924646294357666924293908418345508902112711075232047998775303603175363964055048589769318562104883659754974955561725694779754279606726358588862479198815999276839234952142017210593887371950645418417355912567987
c13 = 3788529784248255027081674540877016372807848222776887920453488878247137930578296797437647922494510483767651150492933356093288965943741570268943861987024276610712717409139946409513963043114463933146088430004237747163422802959250296602570649363016151581364006795894226599584708072582696996740518887606785460775851029814280359385763091078902301957226484620428513604630585131511167015763190591225884202772840456563643159507805711004113901417503751181050823638207803533111429510911616160851391754754434764819568054850823810901159821297849790005646102129354035735350124476838786661542089045509656910348676742844957008857457

n14 = 27545937603751737248785220891735796468973329738076209144079921449967292572349424539010502287564030116831261268197384650511043068738911429169730640135947800885987171539267214611907687570587001933829208655100828045651391618089603288456570334500533178695238407684702251252671579371018651675054368606282524673369983034682330578308769886456335818733827237294570476853673552685361689144261552895758266522393004116017849397346259119221063821663280935820440671825601452417487330105280889520007917979115568067161590058277418371493228631232457972494285014767469893647892888681433965857496916110704944758070268626897045014782837
c14 = 14069112970608895732417039977542732665796601893762401500878786871680645798754783315693511261740059725171342404186571066972546332813667711135661176659424619936101038903439144294886379322591635766682645179888058617577572409307484708171144488708410543462972008179994594087473935638026612679389759756811490524127195628741262871304427908481214992471182859308828778119005750928935764927967212343526503410515793717201360360437981322576798056276657140363332700714732224848346808963992302409037706094588964170239521193589470070839790404597252990818583717869140229811712295005710540476356743378906642267045723633874011649259842

n15 = 25746162075697911560263181791216433062574178572424600336856278176112733054431463253903433128232709054141607100891177804285813783247735063753406524678030561284491481221681954564804141454666928657549670266775659862814924386584148785453647316864935942772919140563506305666207816897601862713092809234429096584753263707828899780979223118181009293655563146526792388913462557306433664296966331469906428665127438829399703002867800269947855869262036714256550075520193125987011945192273531732276641728008406855871598678936585324782438668746810516660152018244253008092470066555687277138937298747951929576231036251316270602513451
c15 = 17344284860275489477491525819922855326792275128719709401292545608122859829827462088390044612234967551682879954301458425842831995513832410355328065562098763660326163262033200347338773439095709944202252494552172589503915965931524326523663289777583152664722241920800537867331030623906674081852296232306336271542832728410803631170229642717524942332390842467035143631504401140727083270732464237443915263865880580308776111219718961746378842924644142127243573824972533819479079381023103585862099063382129757560124074676150622288706094110075567706403442920696472627797607697962873026112240527498308535903232663939028587036724

n16 = 23288486934117120315036919418588136227028485494137930196323715336208849327833965693894670567217971727921243839129969128783853015760155446770590696037582684845937132790047363216362087277861336964760890214059732779383020349204803205725870225429985939570141508220041286857810048164696707018663758416807708910671477407366098883430811861933014973409390179948577712579749352299440310543689035651465399867908428885541237776143404376333442949397063249223702355051571790555151203866821867908531733788784978667478707672984539512431549558672467752712004519300318999208102076732501412589104904734983789895358753664077486894529499
c16 = 10738254418114076548071448844964046468141621740603214384986354189105236977071001429271560636428075970459890958274941762528116445171161040040833357876134689749846940052619392750394683504816081193432350669452446113285638982551762586656329109007214019944975816434827768882704630460001209452239162896576191876324662333153835533956600295255158377025198426950944040643235430211011063586032467724329735785947372051759042138171054165854842472990583800899984893232549092766400510300083585513014171220423103452292891496141806956300396540682381668367564569427813092064053993103537635994311143010708814851867239706492577203899024

n17 = 19591441383958529435598729113936346657001352578357909347657257239777540424811749817783061233235817916560689138344041497732749011519736303038986277394036718790971374656832741054547056417771501234494768509780369075443550907847298246275717420562375114406055733620258777905222169702036494045086017381084272496162770259955811174440490126514747876661317750649488774992348005044389081101686016446219264069971370646319546429782904810063020324704138495608761532563310699753322444871060383693044481932265801505819646998535192083036872551683405766123968487907648980900712118052346174533513978009131757167547595857552370586353973
c17 = 3834917098887202931981968704659119341624432294759361919553937551053499607440333234018189141970246302299385742548278589896033282894981200353270637127213483172182529890495903425649116755901631101665876301799865612717750360089085179142750664603454193642053016384714515855868368723508922271767190285521137785688075622832924829248362774476456232826885801046969384519549385428259591566716890844604696258783639390854153039329480726205147199247183621535172450825979047132495439603840806501254997167051142427157381799890725323765558803808030109468048682252028720241357478614704610089120810367192414352034177484688502364022887

n18 = 19254242571588430171308191757871261075358521158624745702744057556054652332495961196795369630484782930292003238730267396462491733557715379956969694238267908985251699834707734400775311452868924330866502429576951934279223234676654749272932769107390976321208605516299532560054081301829440688796904635446986081691156842271268059970762004259219036753174909942343204432795076377432107630203621754552804124408792358220071862369443201584155711893388877350138023238624566616551246804054720492816226651467017802504094070614892556444425915920269485861799532473383304622064493223627552558344088839860178294589481899206318863310603
c18 = 6790553533991297205804561991225493105312398825187682250780197510784765226429663284220400480563039341938599783346724051076211265663468643826430109013245014035811178295081939958687087477312867720289964506097819762095244479129359998867671811819738196687884696680463458661374310994610760009474264115750204920875527434486437536623589684519411519100170291423367424938566820315486507444202022408003879118465761273916755290898112991525546114191064022991329724370064632569903856189236177894007766690782630247443895358893983735822824243487181851098787271270256780891094405121947631088729917398317652320497765101790132679171889

n19 = 26809700251171279102974962949184411136459372267620535198421449833298448092580497485301953796619185339316064387798092220298630428207556482805739803420279056191194360049651767412572609187680508073074653291350998253938793269214230457117194434853888765303403385824786231859450351212449404870776320297419712486574804794325602760347306432927281716160368830187944940128907971027838510079519466846176106565164730963988892400240063089397720414921398936399927948235195085202171264728816184532651138221862240969655185596628285814057082448321749567943946273776184657698104465062749244327092588237927996419620170254423837876806659
c19 = 386213556608434013769864727123879412041991271528990528548507451210692618986652870424632219424601677524265011043146748309774067894985069288067952546139416819404039688454756044862784630882833496090822568580572859029800646671301748901528132153712913301179254879877441322285914544974519727307311002330350534857867516466612474769753577858660075830592891403551867246057397839688329172530177187042229028685862036140779065771061933528137423019407311473581832405899089709251747002788032002094495379614686544672969073249309703482556386024622814731015767810042969813752548617464974915714425595351940266077021672409858645427346

n=[n0,n1,n2,n3,n4,n5,n6,n7,n8,n9,n10,n11,n12,n13,n14,n15,n16,n17,n18,n19]
c=[c0,c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15,c16,c17,c18,c19]

for i in range(len(n)):
    for j in range(len(n)):
        if(i!=j):
            if(gmpy2.gcd(n[i],n[j])!=1):   #对不同的n进行 欧几里得算法，以求出最大公约数(p)
                print(i,j)                 #输出对应的n的序号            
                p = gmpy2.gcd(n[i],n[j])
                print("p = ",p)
                q = n[i] // p
                print("q = ",q)
                d = gmpy2.invert(e , (p-1)*(q-1))
                print("d = ",d)
                m = pow(c[i],d,n[i])
                print("m = ",m)
# 4 17
# p =  132585806383798600305426957307612567604223562626764190211333136246643723811046149337852966828729052476725552361132437370521548707664977123165279305052971868012755509160408641100548744046621516877981864180076497524093201404558036301820216274968638825245150755772559259575544101918590311068466601618472464832499
# q =  172130338499326278748088659642118539903263306644625489813269854049704514120598134934786316771912260248369075948864036229605563950070491992643125838594149381631362120542615545158696925360916086470107987771246645459433841320759048661246016875180635458357799131806734777129141845728102816378815607663660131827433
# d =  10255762274410447979846484489272592025276530212873111105713911284717751198023145855606019924577798738695538597187877966993598709672960993516539454197162664114978503222530508768362729378865140035425026175847611448858053529432493784291104132035847332081780017599698552936076497425709781734095556186428757196589872934330029936289432604149394663566703657427009973329681704667429413105717095832162998561559367314637614478597021229692702783695719313128949842371770106722991377377048130193746157144666295125327151620068015029385410313912716206956605407434839741405536764244140055959056916717996815600672095481030331533580401
# m =  13040004482825176402070107903979416267670062118522537076883968693524598900675425175282673277
print(libnum.n2s(int(m)))
#b'flag{abdcbe5fd94e23b3de429223ab9c2fdf}'

[NCTF2019]childRSA(费马小定理)

from random import choice
from Crypto.Util.number import isPrime, sieve_base as primes
from flag import flag

def getPrime(bits):
    while True:
        n = 2
        while n.bit_length() < bits:
            n *= choice(primes)
        if isPrime(n + 1):
            return n + 1

e = 0x10001
m = int.from_bytes(flag.encode(), 'big')
p, q = [getPrime(2048) for _ in range(2)]
n = p * q
c = pow(m, e, n)

# n = 32849718197337581823002243717057659218502519004386996660885100592872201948834155543125924395614928962750579667346279456710633774501407292473006312537723894221717638059058796679686953564471994009285384798450493756900459225040360430847240975678450171551048783818642467506711424027848778367427338647282428667393241157151675410661015044633282064056800913282016363415202171926089293431012379261585078566301060173689328363696699811123592090204578098276704877408688525618732848817623879899628629300385790344366046641825507767709276622692835393219811283244303899850483748651722336996164724553364097066493953127153066970594638491950199605713033004684970381605908909693802373826516622872100822213645899846325022476318425889580091613323747640467299866189070780620292627043349618839126919699862580579994887507733838561768581933029077488033326056066378869170169389819542928899483936705521710423905128732013121538495096959944889076705471928490092476616709838980562233255542325528398956185421193665359897664110835645928646616337700617883946369110702443135980068553511927115723157704586595844927607636003501038871748639417378062348085980873502535098755568810971926925447913858894180171498580131088992227637341857123607600275137768132347158657063692388249513
# c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108

只在基础的RSA上修改了大素数的生成过程。choice()函数从小于10000的素数中随机挑选一个

1	这里primes为前10000个素数的列表

p,q的生成方式是一个突破口，分析函数getprime(),p,q就是在前10000个素数列表里面随机找几个素数相乘再加一得到的，所以这10000个素数的乘积x是p-1和q-1的倍数,x=k*(p-1),n=p*q，这里就要从n和x得到p。

费马小定理

1	若b为一个素数，则对于任意整数a，有a^(b-1) = 1 (mod b),即a^k*(b-1) = 1 (mod b)

x=k*(p-1),n=p*q

2^k*(p-1)=1 mod p

2^k*(p-1)-1=k*p

2^x-1=k*p

这里2^x-1是p的倍数，n也是p的倍数，他们的公因数就是p。
用gcd(2^x-1,n)=p,但是x太大了，直接计算公因数运行时间太久了。
我是这样想的p比n小，把2^x-1 mod n 再求公因数应该也可以吧。
下面看看证明：
2^x= 1 (mod p)，即2^x = 1 + k1*p
而2^x% n = 2^x - k2n = 2^x - k2pq
两边同时% p，有2^x% n = 2^x (mod p)
所以同样有2^x % n = 1 (mod p)

import gmpy2
import libnum
from Crypto.Util.number import isPrime, sieve_base as primes
 
c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108
n=32849718197337581823002243717057659218502519004386996660885100592872201948834155543125924395614928962750579667346279456710633774501407292473006312537723894221717638059058796679686953564471994009285384798450493756900459225040360430847240975678450171551048783818642467506711424027848778367427338647282428667393241157151675410661015044633282064056800913282016363415202171926089293431012379261585078566301060173689328363696699811123592090204578098276704877408688525618732848817623879899628629300385790344366046641825507767709276622692835393219811283244303899850483748651722336996164724553364097066493953127153066970594638491950199605713033004684970381605908909693802373826516622872100822213645899846325022476318425889580091613323747640467299866189070780620292627043349618839126919699862580579994887507733838561768581933029077488033326056066378869170169389819542928899483936705521710423905128732013121538495096959944889076705471928490092476616709838980562233255542325528398956185421193665359897664110835645928646616337700617883946369110702443135980068553511927115723157704586595844927607636003501038871748639417378062348085980873502535098755568810971926925447913858894180171498580131088992227637341857123607600275137768132347158657063692388249513
e=0x10001
x=1
for i in primes:
    x=i*x
 
p=gmpy2.gcd(pow(2,x,n)-1,n)
q=n//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
flag=libnum.n2s(int(m))
print(flag)
# b'NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}'

总结：当知道某一个数x是p-1,q-1的倍数时，就用gcd(2^x-1,n)=p，进一步gcd(pow(2,x,n)-1,n)=p。

[HDCTF2019]bbbbbbrsa

可以明显的看到c是逆过来的，我们重新把c进行排序，在进行base64解码得到c

from base64 import b64encode as b32encode
from base64 import b64decode
from gmpy2 import invert, gcd, iroot
from Crypto.Util.number import *

p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c64 = '==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM'
c = int(b64decode(str(c64)[::-1]))
print(c)
q = n // p
phi = (p - 1) * (q - 1)
for e in range(50000, 70000):
	if gcd(e, phi) == 1:
		d = invert(e, phi)
		m = pow(c, d, n)
		flag = str(long_to_bytes(m))
		if 'flag' in flag or 'CTF' in flag or ("{" in flag and '}' in flag):
			print(flag)

rsa4(低加密指数广播攻击)

另外有两点需要注意：
1、此题中的N、c均是以5进制表示，要先用int(“*****”,5)转换为十进制才能计算(开始运行半天都不出结果，看了其他师傅博客才发现原来是五进制)。
2、题目没有给出加密指数e，但是根据低加密指数广播攻击的特性猜e=3、10、17等

from Crypto.Util.number import *
import primefac
import gmpy2

e = 3

def modinv(a,n):
    return primefac.modinv(a,n) % n

def CRT(n1,c1,n2,c2,n3,c3):
    n = n1*n2*n3
    m_e = 0
    m_e = m_e + c1*(n2*n3)*modinv(n2*n3,n1)
    m_e = m_e + c2*(n1*n3)*modinv(n1*n3,n2)
    m_e = m_e + c3*(n1*n2)*modinv(n2*n1,n3)
    return m_e % n

n1 = int('331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004',5)
c1 = int('310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243',5)
n2 = int('302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114',5)
c2 = int('112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344',5)
n3 = int('332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323',5)
c3 = int('10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242',5)
m_e = CRT(n1,c1,n2,c2,n3,c3)
m = gmpy2.iroot(m_e,e)[0]
print(long_to_bytes(m))

primefac.modinv(a, n): 这个部分使用primefac库中的modinv函数，来计算a在模n意义下的逆元素。这意味着找到一个数x，使得 (a * x) % n = 1

[BJDCTF2020]rsa_output

我们审计题目，发现题目给了我们两个一样的m和两个不一样的e和c，我们考虑共模攻击，

c1 = m^e1 mod n =>c1^s1 = m^(e1*s1) mod n

c2 = m^e2 mod n =>c2^s2 = m^(e2*s2) mod n

两者相乘，通过扩展欧几里得定理，我们可知e1与e2互质，必存在s1和s2使e1s1+e2s2=1

由此可求出相对应的s1和s2.

m=（c1*s1+c2*s2）%n

n=21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111
e1=2767
e2=3659
c1=20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599
c2=11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227
 
#已知两者n相同，e不同，共模攻击
 
import gmpy2
from Crypto.Util.number import isPrime, sieve_base as primes,long_to_bytes
 
def egcd(a,b):
    if b==0:
        return a,0;
    else:
        x,y=egcd(b,a%b)
        return y,x-(a//b)*y #扩展欧几里得算法
 
s=egcd(e1,e2)
s1=s[0]
s2=s[1]
print(s[0],s[1])
m = gmpy2.powmod(c1, s1, n) *gmpy2.powmod(c2, s2, n) % n
 
print(long_to_bytes(m))

//

[BJDCTF2020]RSA

from Crypto.Util.number import getPrime,bytes_to_long

flag=open("flag","rb").read()

p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)

p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n

我们发现第一个n和第二个n共用一个q，因此我们通过gcd可以得到q的值，从而得到p的值，又已知pow(294,e,n)的值，因此我们可以爆破出e的值

from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
from math import gcd
from gmpy2 import invert
c=12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n=13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
a=381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
BJDc=979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721
BJDn=12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
q=gcd(n,BJDn)
p=n//q
phi=(p-1)*(q-1)
e=0
for i in range(100000):
    if pow(294,i,n)==a:
        print(i)
        e=i
        break

d=invert(e,phi)
m=pow(c,d,n)
print(long_to_bytes(m))

[GWCTF 2019]BabyRSA(解方程)

import hashlib
import sympy
from Crypto.Util.number import *

flag = 'GWHT{******}'
secret = '******'

assert(len(flag) == 38)

half = len(flag) / 2

flag1 = flag[:half]
flag2 = flag[half:]

secret_num = getPrime(1024) * bytes_to_long(secret)

p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)
//说明p,q接近，可用yafu求解

N = p * q

e = 0x10001

F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)
//flag被加密

c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
//设方程组，可解F1，F2
assert(c2 < N)

m1 = pow(c1, e, N)
m2 = pow(c2, e, N)
可逆模求c1，c2

output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()

求得p和q

接着求d

1	d=gmpy2.invert(e,(p-1)*(q-1))

然后可以求c1,c2

1 2	c1=pow(m1,d,N) c2=pow(m2,d,N)

然后联立方程，求得F1，F2

F1=Symbol('F1')
F2=Symbol('F2')
x = F1 + F2-c1
y = pow(F1, 3) + pow(F2, 3)-c2
a=solve([x,y],[F1,F2])

最后转为字节

import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes
from sympy import *
e=0x10001
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
p=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
q=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699
d=gmpy2.invert(e,(p-1)*(q-1))
c1=pow(m1,d,N)
c2=pow(m2,d,N)
F1=Symbol('F1')
F2=Symbol('F2')
x = F1 + F2-c1
y = pow(F1, 3) + pow(F2, 3)-c2
a=solve([x,y],[F1,F2])
#F1=1590956290598033029862556611630426044507841845
#F2=1141553212031156130619789508463772513350070909
print(long_to_bytes(F1)+long_to_bytes(F2))
#b'GWHT{f709e0e2cfe7e530ca8972959a1033b2}'

SameMod（共模攻击）

模攻击

共模是指：就是明文m,相同。用两个公钥e1,e2加密得到两个私钥d1,d2 和两个密文c1,c2

共模攻击，即当m不变的情况下，知道n,e1,e2,c1,c2, 可以在不知道d1,d2的情况下，解出m

利用条件为=> gcd(e1,e2)=1

根据扩展欧几里得算法得

可以得到该式子的一组解(s1,s2) 假设s1为正数，s2为负数

有整数s1,s2(一正一负)

存在e1s1+e2s2==1

from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext

n=6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
e1=773
e2=839
c1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
c2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
s,s1,s2=gcdext(e1,e2)
m = ((pow(c1,s1,n)*pow(c2,s2,n)) % n)
print(m)
print(long_to_bytes(m))

我们发现输出是一串乱码，但当我们看到m的值，发现里面有ascii码的影子

我们进行解码

from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext

n=6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
e1=773
e2=839
c1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
c2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
s,s1,s2=gcdext(e1,e2)
m = str((pow(c1,s1,n)*pow(c2,s2,n)) % n)
print(m)

flag=""
i=0
while i < len(m):
    if m[i]=='1':
        c=chr(int(m[i:i+3]))
        i+=3
    else:
        c=chr(int(m[i:i+2]))
        i+=2
    flag+=c

print(flag)

得到flag

[AFCTF2018]可怜的RSA（rsa公钥加密）

我们先利用Crypto.PublicKey的RSA模块从key文件中获取公钥信息n,e

from Crypto.PublicKey import RSA
f = open("C:\\Users\\11\\Downloads\\attachment\public.key","rb").read()
pub = RSA.importKey(f)
print(pub.n,pub.e)

# n = 79832181757332818552764610761349592984614744432279135328398999801627880283610900361281249973175805069916210179560506497075132524902086881120372213626641879468491936860976686933630869673826972619938321951599146744807653301076026577949579618331502776303983485566046485431039541708467141408260220098592761245010678592347501894176269580510459729633673468068467144199744563731826362102608811033400887813754780282628099443490170016087838606998017490456601315802448567772411623826281747245660954245413781519794295336197555688543537992197142258053220453757666537840276416475602759374950715283890232230741542737319569819793988431443
# e = 65537

得到n，e的值后，对n进行分解，得到p和q

1
2

p = 3133337
q = 25478326064937419292200172136399497719081842914528228316455906211693118321971399936004729134841162974144246271486439695786036588117424611881955950996219646807378822278285638261582099108339438949573034101215141156156408742843820048066830863814362379885720395082318462850002901605689761876319151147352730090957556940842144299887394678743607766937828094478336401159449035878306853716216548374273462386508307367713112073004011383418967894930554067582453248981022011922883374442736848045920676341361871231787163441467533076890081721882179369168787287724769642665399992556052144845878600126283968890273067575342061776244939

利用gmpy2库通过p,q,ep,q,e求d

from gmpy2 import *
d = int(invert(e, (p-1)*(q-1)))
print(d)
# d = 406853230956379689450620815713768871010712825839536410687962650677800895818003893712259622281477453292088146173840036827322518131453630576229976208523593618949818777897059256426591560532784635697190752924923710375949616954069804342573867253630978123632384795587951365482103468722384133084798614863870775897915929475258974188300927376911833763105616386167881813301748585233563049693794370642976326692672223638908164822104832415788577945314264232531947860576966629150456995512932232264881080618006698700677529111454508900582785420549466798020451488168615035256292977390692401388790460066327347700109341639992159475755036449

打包密钥对flag.pnc解密（由于是Base64编码后的密文，因此还需解码）

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from base64 import b64decode
key_info = RSA.construct((n, e, d, p, q))
key = RSA.importKey(key_info.exportKey())
key = PKCS1_OAEP.new(key)
f = open('D:\\Download\\flag.enc', 'r').read()
c = b64decode(f)
flag = key.decrypt(c)
print(flag)

[RoarCTF2019]babyRSA(威尔逊定理)

import sympy
import random

def myGetPrime():
    A= getPrime(513)
    print(A)
    B=A-random.randint(1e3,1e5)
    print(B)
    return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
#B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596

q=myGetPrime()
#A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
#B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026

r=myGetPrime()

n=p*q*r
#n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c=pow(flag,e,n)
#e=0x1001
#c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
#so,what is the flag?

分析
从代码中可以知道：

p=(B1!)%A1p=(B1!)%A1

q=(B2!)%A2q=(B2!)%A2

又由威尔逊定理知道，

(A−1)!≡ −1 mod A(A−1)!≡ −1 mod A

而B=A-random.randint(1e3,1e5)，所以在B的前面补上

(A−1)(A−2)(A−3)…(B+1)(A−1)(A−2)(A−3)…(B+1)

就有

(A−1)(A−2)(A−3)…(B+1)∗(B!)%A=−1%A(A−1)(A−2)(A−3)…(B+1)∗(B!)%A=−1%A

于是再整理一下又有

(A−2)(A−3)…(B+1)∗(B!)%A=1%A(A−2)(A−3)…(B+1)∗(B!)%A=1%A

这就意味这可由(A−2)(A−3)…(B+1)(A−2)(A−3)…(B+1)模A的逆元求得(B!)%A(B!)%A的值。再取nextprime(sympy.ntheory.generate模块里的nextprime不是nextPrime)即可得到p或q的值。

from sympy import nextprime
from Crypto.Util.number import *
from gmpy2 import invert

def get_p_q(A,B):
    tmp = 1
    # calculate remain value (mod A) of (A−1)(A−2)(A−3)...(B+1)
    for i in range(B+1,A-1):
        tmp *= i
        tmp %= A

    tmp_inv = invert(tmp,A)
    result = nextprime(tmp_inv)
    return result

A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596

A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026

n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
e=0x1001
c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428

p = get_p_q(A1,B1)
q = get_p_q(A2,B2)
print(p)
print(q)
# p = 1276519424397216455160791032620569392845781005616561979809403385593761615670426423039762716291920053306063214548359656555809123127361539475238435285654851
# q = 13242175493583584108411324143773780862426183382017753129633978933213674770487765387985282956574197274056162861584407275172775868763712231230219112670015751

r = n // p // q
print(r)
# r = 5057572094237208127867754008134739503717927865750318894982404287656747895573075881186030840558129423864679886646066477437020450654848839861455661385205433

phn = (p - 1) * (q - 1) * (r - 1)
d = invert(e, phn)
print(d)
# d = 23245991568931089935575398139533179902151911325504278186895368123724684132878362590745372016987963378102056924287587028702166372731411906405181410326380814220943063812165970658883369631308421395770179828382024820676516261188276456737434776404340381374859304944884947772697915445301641449023374627214573292539161320959779418043275889202421521069705878414823578781441160766914068377017428380775625886023385019623499784980822629415795884228504498888092721097658433
m = pow(c,d,n)
print(m)
# 49562188096458630410563044417358818341913265571373725266976612126526106528404944745044614126232074073813936259453
print(long_to_bytes(m))

RoarCTF{wm-CongrAtu1ation4-1t4-ju4t-A-bAby-R4A}

RSA & what（共模攻击&base64隐写）

我们仔细观察两个文件，发现有两个e和多个c，n是一样的，我们想到共模攻击

from Crypto.Util.number import*
import base64

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def CMA(n,e1,e2,c1,c2):
    s = egcd(e1, e2)
    s1 = s[1]
    s2 = s[2]
    if s1<0:
        s1 = - s1
        c1 = inverse(c1, n)
    elif s2<0:
        s2 = - s2
        c2 = inverse(c2, n)
    m = pow(c1,s1,n)*pow(c2,s2,n) % n
    return m

f1=open("C:\\Users\\11\\Downloads\\2e37d2da-1cda-45a5-bb73-413c37864fa1\\rsawhat\\HUB1")
f2=open("C:\\Users\\11\\Downloads\\2e37d2da-1cda-45a5-bb73-413c37864fa1\\rsawhat\\HUB2")
N=f1.readline()
N=f2.readline()
e1,e2=f1.readline(),f2.readline()
f1.readline()
f2.readline()
c1,c2=f1.readline(),f2.readline()
ans=b''
cnt=0
while len(c1)!=0:
    cnt+=1
    ans+=long_to_bytes(CMA(int(N),int(e1),int(e2),int(c1),int(c2)))
    #print(base64.b64decode(temp))
    c1,c2=f1.readline(),f2.readline()
temp=b''
M=b''
print(ans)
for i in ans:
    k=long_to_bytes(i)
    #print(i," ",end="")
    if k==b'\n':
        M+=base64.b64decode(temp)
        temp=b''
        continue
    temp+=k
print(M)

得到的明文为base64编码，解码后是对base54的介绍，没啥用

我们主要看base64编码是一段一段的

不难想到base64隐写。

我们到网上找一段base64隐写脚本

from Crypto.Util.number import*
import base64
c = b'VEhJUz==\nRkxBR3==\nSVN=\nSElEREVOLo==\nQ0FO\nWU9V\nRklORM==\nSVT=\nT1VUP4==\nRE8=\nWU9V\nS05PV9==\nQkFTRTY0P5==\nWW91bmdD\nVEhJTku=\nWU9V\nQVJF\nTk9U\nVEhBVE==\nRkFNSUxJQVI=\nV0lUSO==\nQkFTRTY0Lh==\nQmFzZTY0\naXO=\nYW==\nZ3JvdXA=\nb2b=\nc2ltaWxhcn==\nYmluYXJ5LXRvLXRleHR=\nZW5jb2Rpbme=\nc2NoZW1lc0==\ndGhhdD==\ncmVwcmVzZW50\nYmluYXJ5\nZGF0YW==\naW5=\nYW6=\nQVNDSUl=\nc3RyaW5n\nZm9ybWF0\nYnk=\ndHJhbnNsYXRpbmd=\naXS=\naW50b1==\nYT==\ncmFkaXgtNjQ=\ncmVwcmVzZW50YXRpb24u\nVGhl\ndGVybc==\nQmFzZTY0\nb3JpZ2luYXRlc8==\nZnJvbd==\nYY==\nc3BlY2lmaWN=\nTUlNRT==\nY29udGVudI==\ndHJhbnNmZXI=\nZW5jb2Rpbmcu\nVGhl\ncGFydGljdWxhct==\nc2V0\nb2b=\nNjR=\nY2hhcmFjdGVyc5==\nY2hvc2Vu\ndG+=\ncmVwcmVzZW50\ndGhl\nNjQ=\ncGxhY2UtdmFsdWVz\nZm9y\ndGhl\nYmFzZd==\ndmFyaWVz\nYmV0d2Vlbt==\naW1wbGVtZW50YXRpb25zLp==\nVGhl\nZ2VuZXJhbI==\nc3RyYXRlZ3n=\naXO=\ndG9=\nY2hvb3Nl\nNjR=\nY2hhcmFjdGVyc5==\ndGhhdA==\nYXJl\nYm90aN==\nbWVtYmVyc5==\nb2a=\nYS==\nc3Vic2V0\nY29tbW9u\ndG8=\nbW9zdM==\nZW5jb2RpbmdzLA==\nYW5k\nYWxzb8==\ncHJpbnRhYmxlLg==\nVGhpc9==\nY29tYmluYXRpb25=\nbGVhdmVz\ndGhl\nZGF0YW==\ndW5saWtlbHk=\ndG/=\nYmV=\nbW9kaWZpZWS=\naW5=\ndHJhbnNpdE==\ndGhyb3VnaN==\naW5mb3JtYXRpb26=\nc3lzdGVtcyw=\nc3VjaN==\nYXM=\nRS1tYWlsLD==\ndGhhdA==\nd2VyZQ==\ndHJhZGl0aW9uYWxseQ==\nbm90\nOC1iaXQ=\nY2xlYW4uWzFd\nRm9y\nZXhhbXBsZSw=\nTUlNRSdz\nQmFzZTY0\naW1wbGVtZW50YXRpb24=\ndXNlcw==\nQahDWiw=\nYahDeiw=\nYW5k\nMKhDOQ==\nZm9y\ndGhl\nZmlyc3Q=\nNjI=\ndmFsdWVzLg==\nT3RoZXI=\ndmFyaWF0aW9ucw==\nc2hhcmU=\ndGhpcw==\ncHJvcGVydHk=\nYnV0\nZGlmZmVy\naW4=\ndGhl\nc3ltYm9scw==\nY2hvc2Vu\nZm9y\ndGhl\nbGFzdA==\ndHdv\ndmFsdWVzOw==\nYW4=\nZXhhbXBsZQ==\naXM=\nVVRGLTcu'

def get_base64_diff_value(s1, s2):
    base64chars = b'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
    res = 0
    for i in range(len(s2)):
        if s1[i] != s2[i]:
            return abs(base64chars.index(s1[i]) - base64chars.index(s2[i]))
    return res

def solve_stego():
    line=b''
    bin_str=''
    for i in c:
        k=long_to_bytes(i)
        if k==b'\n':
            steg_line = line
            norm_line = base64.b64encode(base64.b64decode(line))
            diff = get_base64_diff_value(steg_line, norm_line)
            #print(diff)
            pads_num = steg_line.count(b'=')
            if diff:
                bin_str += bin(diff)[2:].zfill(pads_num * 2)
            else:
                bin_str += '0' * pads_num * 2
            print(goflag(bin_str))
            line=b''
            continue
        line+=k

def goflag(bin_str):
    res_str = ''
    for i in range(0, len(bin_str), 8):
        res_str += chr(int(bin_str[i:i + 8], 2))
    return res_str


if __name__ == '__main__':
    solve_stego()

//7c86d8f7d6de33a87f7f9d6b005ce640

flag吧数字包起来就行了

[NPUCTF2020]EzRSA（最小公倍数(p,q) ∗ 最大公因数(p,q) = p∗q）

根据题设，我们得到以下关系

gift=lcm((p-1)*(q-1)) 
gmpy2.lcm求最小公倍数
n=p*q
c=m^e mod n

由小学五年级的知识，有

1	最小公倍数(p,q) ∗ 最大公因数(p,q) = p∗q

所以对于gift

有

我们可以求的gift的二进制位数为2045

1	print(len(bin(gift)[2:]))

同时我们知道ϕ(n)的位数为2048，因此gcd(p−1,q−1)gcd(p−1,q−1)占3bits，因此最大公因数的范围（十进制）为[4,8]

我们在此范围内遍历最大公因数的值，然后与最小公倍数相乘得到ϕ(n)的值，然后通过逆模运算求得d，然后就可得·明文

但需要注意这里的e不是素数，分解可得e=2*27361

所以在计算时，我们要先将e除以2

值的变化可通过以下表达式体现

所以解出的明文需要开根号再转为字节流

注意：遍历过程中不是所有的值都符合条件，可能会报ZeroDivisionError，因此需要加异常处理

from Crypto.Util.number import *
import gmpy2

e = 54722
# e = 2*27361
n = 17083941230213489700426636484487738282426471494607098847295335339638177583685457921198569105417734668692072727759139358207667248703952436680183153327606147421932365889983347282046439156176685765143620637107347870401946946501620531665573668068349080410807996582297505889946205052879002028936125315312256470583622913646319779125559691270916064588684997382451412747432722966919513413709987353038375477178385125453567111965259721484997156799355617642131569095810304077131053588483057244340742751804935494087687363416921314041547093118565767609667033859583125275322077617576783247853718516166743858265291135353895239981121
gift = 2135492653776686212553329560560967285303308936825887355911916917454772197960682240149821138177216833586509090969892419775958406087994054585022894165950768427741545736247918410255804894522085720642952579638418483800243368312702566458196708508543635051350999572787188236243275631609875253617015664414032058822919469443284453403064076232765024248435543326597418851751586308514540124571309152787559712950209357825576896132278045112177910266019741013995106579484868768251084453338417115483515132869594712162052362083414163954681306259137057581036657441897428432575924018950961141822554251369262248368899977337886190114104
c = 3738960639194737957667684143565005503596276451617922474669745529299929395507971435311181578387223323429323286927370576955078618335757508161263585164126047545413028829873269342924092339298957635079736446851837414357757312525158356579607212496060244403765822636515347192211817658170822313646743520831977673861869637519843133863288550058359429455052676323196728280408508614527953057214779165450356577820378810467527006377296194102671360302059901897977339728292345132827184227155061326328585640019916328847372295754472832318258636054663091475801235050657401857262960415898483713074139212596685365780269667500271108538319
# gift = 8 * 11 * 97 * 9601 * 26057167557433418766727399341516665922795024485718296827775927226598694152064298989740080209950805089159979564300359652085874056289167084685303669920341402021998569251561854184586912056788515477034039863935829715784489123437315798902409373317578932823488000322365526936227790036245092665207472438169954702748857842187299166976320465787901470261800372425345547560303561842376571751928531743505412746346436473024093575122041981043859827477404447458211341273671273506575488189374812217939984540494633634622813448773520886788206836310702581026986331011987344147901504555559723572981774237352245997308787165273589

print(len(bin(gift)[2:]))
print(len(bin(n)[2:]))

# gift * gcd = (p-1) * (q-1)
# gift % gcd = 0
for gcd_val in range(4, 8):
    phi = gift * gcd_val
    try:
        d = gmpy2.invert(e // 2, phi)
        m_2 = pow(c, int(d), n)
        flag = long_to_bytes(gmpy2.isqrt(m_2))
        print(flag)
    except ZeroDivisionError:
        continue

//NPUCTF{diff1cult_rsa_1s_e@sy}

[MRCTF2020]babyRSA

由 gen_q()函数我们可以直接得出_Q的值：

1 2	Q = sub_Q ** Q_2 % Q_1 _Q= sympy.nextprime(Q)

我们观察gen_p

def gen_p():
    P = [0 for i in range(17)]
    P[0] = getPrime(128)
    for i in range(1, 17):
        P[i] = sympy.nextprime(P[i-1])
    print("P_p :", P[9])
    n = 1
    for i in range(17):
        n *= P[i]
    p = getPrime(1024)
    factor = pow(p, base, n)
    print("P_factor :", factor)
    return sympy.nextprime(p)

它通过循环生成了17个素数，并且给了第九个素数的值，我们可以逆推和顺推得到其余16个素数的值

然后n将17个素数乘在一起

有欧拉函数

那我们就可以得到_p的值

既然已知_Q和_P,我们就能得到flag

import gmpy2
from Crypto.Util.number import long_to_bytes
import sympy
base = 65537
P_p =206027926847308612719677572554991143421
P_factor=213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
Q_1=103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2=151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q=168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Ciphertext =  1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832
Q = pow(sub_Q,Q_2,Q_1)
_Q=sympy.nextprime(Q)
n=1
#print(_Q)
def p_prime(p):
    while 1:
        p=p-2
        if(sympy.isprime(p)):
            return p


#_Q=95170653714081687088760585440906768700419459767774333757336842864507607081809193370870747769993218256925111100260761958233280546585624501259121060195932474781731613458132842656517609786144352755126076860272047457230913808406105832246663969943550533958139118721153456230616182820319799156494938586844573835221
P = [0 for i in range(17)]
P[9]=206027926847308612719677572554991143421
for i in range(10,17):
    P[i]=sympy.nextprime(P[i-1])
for i in range(9,0,-1):
    P[i-1]=p_prime(P[i])
for i in range(17):
    n*=P[i]
phi_1=1
for i in range(17):
    phi_1*=(P[i]-1)
d=gmpy2.invert(base,phi_1)
_P_1=pow(P_factor,d,n)
_P=sympy.nextprime(_P_1)
phi=(_P-1)*(_Q-1)
D=gmpy2.invert(base,phi)
_M=pow(Ciphertext,D,_P*_Q)
print(long_to_bytes(_M))

[MRCTF2020]Easy_RSA

求P：

1 2	n=pq φ(n)=(p-1)(q-1)=p*q-(p+q)+1

已知p+q和p*q，我们就能得到(p+q)和(p-q)的平方，然后开根解方程即可

求Q：

与求P不同：此处无φ(n)，只有Q_E_D，

根据e*d mod φ(n) =1 来求φ(n)

首先：

φ(n)=(p-1)*(q-1)

e*d = kφ(n) +1=k(pq -p -q +1) +1 ==> k = (e * d -1)/(pq - p - q +1)

k值无法确定，上式难以求解。

p,q均为大质数，并且1<< p < q, 那么：

(pq - p - q +1) ≈( p-2)q≈ pq

k = (e * d -1)/(pq - p - q +1) ≈ (Q_E_D -1)/Q_n

由于分母放大，所求k值略小： k = ((Q_E_D-1)//Q_n)+1

则可求解Q

exp

import gmpy2,sympy
from Crypto.Util.number import *
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
e = 65537

def get_fac(n,fai_n):
    p_q_sum = n - fai_n + 1
    difference_square = p_q_sum**2 - 4*n
    difference = gmpy2.iroot(difference_square,2)[0]

    p = (p_q_sum + difference) // 2
    q = p_q_sum - p
    if q < p:
        p,q = q,p
    return p,q

k = (Q_E_D - 1) // Q_n + 1
Q_fai_n = (Q_E_D - 1) // k
P_p,P_q = get_fac(P_n,P_F_n)
Q_p,Q_q = get_fac(Q_n,Q_fai_n)
factor1 = 2021*P_p + 2020*P_q
if factor1 < 0:
    factor1 = (-1) * factor1
P = sympy.nextprime(factor1)
factor2 =  2021*Q_p - 2020*Q_q
if factor2 < 0:
    factor2 = (-1) * factor2
Q = sympy.nextprime(factor2)
fai_n = (P-1)*(Q-1)
D = gmpy2.invert(e,fai_n)
M = pow(Ciphertext,D,P*Q)
print(long_to_bytes(M))

[HDCTF2019]together(base64与unicode之间的转换以及共模攻击)

题目给了四个文件

两个密文，那个公钥

我们先看两个公钥的n和e

我们用kail的openssl进行解码

1 2	openssl rsa -pubin -text -modulus -in warmup -in pubkey1.pem openssl rsa -pubin -text -modulus -in warmup -in pubkey2.pem

或者用python脚本进行读取

from Crypto.PublicKey import RSA
f = open("C:\\Users\\11\\Downloads\\attachment (4)\pubkey2.pem","rb").read()
pub = RSA.importKey(f)
print(pub.n,pub.e)

得到两个公钥的n和e

pubkey1.pem
e1=2333
n1=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299

pubkey2.pem
n2=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299
e2=23333

我们可以发现n相同，但e不同，这里一个考的是共模攻击

然后将my_flag1和my_flag2用随波逐流进行base64转16进制，得到c1和c2

1
2
3

c1=0x52334e6f79367233574c49747974416d6234466d484579676f696c756345455a624f395a595878354a4e3033484e70424c44783766586432666c2b554c352b31315243732f7930716c5447555257574474473636654e4c7a47774e70414b69566a3649375274554a6c3250636d334e764665414677493955735652457968377a4956367349395a50386c2f324756446f724c417a35554c572b66304f494e47684a6d5a6d38464c2f61446e6c6654456c685138374c506963577058596f4d747972365772786a4b364f6e746e384271437430456a51375465585a6878494839565450576a446d46646d4f716171645649542b4c5a656d54674c4e4553774d356e6e346735533361464446776a31596944596c302f2b386574764b664f72666f4b4f7752304378735248616777645555544553384563484c6d4d474378436b445a6e33537a6d6d41364e62336c674c65536747385031413d3d

c2=0x4f2b7252435849336154423650317259494f505564616c557036756a7077457134493230436f57412b48494c38787847747159364e356770723067755a76395a674f45414d466e42784f714d64564e6e423947676e686d587474315a5779645071496348766c667770642f4c79643058536a586e6a617a335033764f517652373163442f75587942413058507a6d6e54494d67456875474a56466d386d696e304c2f3271493777672f5a3777312b346d4f6d693635354a4958654369473233756b4476366c39625a7571664776574361314b4b5857445033316e4c6270305a4e326f625573366a454161317156546158364d344d792b736b732b3056764841547241557543726d4d775645697671494a2f6e5336796d475645524e364f686e7a79723136386b6e45424b4f566a3046414f7833594c6670704d4d2b58624f47486571644b4a524c704d76714658444d4751496e5433773d3d

然后我们进行rsa解密

from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext

c1=0x477368cbaaf758b22dcad0266f81661c4ca0a2296e7041196cef59617c7924dd371cda412c3c7b7d77767e5f942f9fb5d510acff2d2a953194456583b46eba78d2f31b036900a8958fa23b46d5099763dc9b736f15e005c08f54b15444ca1ef3215eac23d64ff25ff61950e8acb033e542d6f9fd0e20d1a1266666f052ff6839e57d3125850f3b2cf89c5a95d8a0cb72afa5abc632ba3a7b67f01a82b7412343b4de5d9871207f554cf5a30e615d98ea9aa9d5484fe2d97a64e02cd112c0ce679f88394b76850c5c23d58883625d3ffbc7adbca7ceadfa0a3b04740b1b111da830754513112f047072e63060b10a40d99f74b39a603a35bde580b792806f0fd4
c2=0x3bead109723769307a3f5ad820e3d475a954a7aba3a7012ae08db40a8580f8720bf31c46b6a63a379829af482e66ff5980e1003059c1c4ea8c75536707d1a09e1997b6dd595b274fa88707be57f0a5dfcbc9dd174a35e78dacf73f7bce42f47bd5c0ffb97c810345cfce69d320c80486e1895459bc9a29f42ffdaa23bc20fd9ef0d7ee263a68bae792485de0a21b6dee903bfa97d6d9baa7c6bd609ad4a2975833f7d672dba7464dda86d4b3a8c401ad6a553697e8ce0ccbeb24b3ed15bc7013ac052e0ab98cc15122bea209fe74baca619511137a3a19f3cabd7af249c404a3958f41403b1dd82dfa6930cf976ce1877aa74a2512e932fa855c33064089d3df
n2=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299
e2=23333
e1=2333
n=14853081277902411240991719582265437298941606850989432655928075747449227799832389574251190347654658701773951599098366248661597113015221566041305501996451638624389417055956926238595947885740084994809382932733556986107653499144588614105694518150594105711438983069306254763078820574239989253573144558449346681620784979079971559976102366527270867527423001083169127402157598183442923364480383742653117285643026319914244072975557200353546060352744263637867557162046429886176035616570590229646013789737629785488326501654202429466891022723268768841320111152381619260637023031430545168618446134188815113100443559425057634959299

s,s1,s2=gcdext(e1,e2)
m=(pow(c1,s1,n)*pow(c2,s2,n))%n
print(long_to_bytes(m))

#b'flag{23re_SDxF_y78hu_5rFgS}'

得到flag

[INSHack2017]rsa16m(低加密指数广播攻击)

通过md文件提示我们可以知道n非常非常非常大

我们推测这题为低密度指数加密攻击，直接将n进行开方

import gmpy2
with open('C:\\rsa_16m',"r") as f:
    f.readline()
    c=int(f.readline().strip("\n").split("=")[1],16)
import libnum
e=65537
m=gmpy2.iroot(c,e)[0]
print(libnum.n2s(int(m)))
f.close()
//b'INSA{(I)NSA_W0uld_bE_pr0uD}'

[NPUCTF2020]认清形势，建立信心

from Crypto.Util.number import *
from gmpy2 import *
from secret import flag

p = getPrime(25)
e = # Hidden
q = getPrime(25)
n = p * q
m = bytes_to_long(flag.strip(b"npuctf{").strip(b"}"))

c = pow(m, e, n)
print(c)
print(pow(2, e, n))
print(pow(4, e, n))
print(pow(8, e, n))

'''
169169912654178
128509160179202
518818742414340
358553002064450
'''

已知

m1 =2^e^ mod n

m2 =2^2e^ mod n

m3 =2^3e^ mod n

我们可得

m2=m1^2^ + k1*n

m3=m1*m2+k2*n

所以 n =gcd(m1^2^-m2,m1*m2-m3)

之后用yafu分解n，正常rsa就行

from Crypto.Util.number import*
from gmpy2 import*
from sympy import*
from libnum import*

c = 169169912654178
c1 = 128509160179202
c2 = 518818742414340
c3 = 358553002064450

n = gcd(pow(c1,2)-c2,c1*c2-c3)
# print(n)
# P1 = 2
p = 28977097
q = 18195301
n = p*q
e = discrete_log(n,c1,2)
#2**e ≡ c1 (mod n)
print(e)
phi = (p-1)*(q-1)
d=  invert(e,phi)
m = n2s(pow(c,int(d),n))
print(m)

discrete_log(n,a,b)

b^x^ ≡ a mod n

在计算离散对数时，要求底数（基数）和模数必须是互质的，即n和b的最大公约数（gcd）应为 1

[De1CTF2019]babyrsa(中国剩余定理&e与phi不互质&低加密&裴蜀定理)

这个题分为四步来写

第一步

代码最上面一层给了4组n和c，估计是中国剩余定理

中国剩余定理的python脚本如下：

import gmpy2
import math
def  merge(a1,n1,a2,n2):
    d = math.gcd(n1,n2)
    c = a2-a1
    if c%d!=0:
        return 0
    c = (c%n2+n2)%n2
    c = c//d
    n1 = n1//d
    n2 = n2//d
    c *= gmpy2.invert(n1,n2)
    c %= n2
    c *= n1*d
    c += a1
    global n3
    global a3
    n3 = n1*n2*d
    a3 = (c%n3+n3)%n3
    return 1
def exCRT(a,n):
    a1=a[0]
    n1=n[0]
    le= len(a)
    for i in range(1,le):
        a2 = a[i]
        n2=n[i]
        if not merge(a1,n1,a2,n2):
            return -1
        a1 = a3
        n1 = n3
    global mod
    mod=n1
    return (a1%n1+n1)%n1
def exCRT_getequation(a,n):
    a1=a[0]
    n1=n[0]
    le= len(a)
    for i in range(1,le):
        a2 = a[i]
        n2=n[i]
        if not merge(a1,n1,a2,n2):
            return -1
        a1 = a3
        n1 = n3
    return (a1,n1)
#a为余数列表
#n为模数列表
n =  [20129615352491765499340112943188317180548761597861300847305827141510465619670536844634558246439230371658836928103063432870245707180355907194284861510906071265352409579441048101084995923962148527097370705452070577098780246282820065573711015664291991372085157016901209114191068574208680397710042842835940428451949500607613634682684113208766694028789275748528254287705759528498986306494267817198340658241873024800336013946294891687591013414935237821291805123285905335762719823771647853378892868896078424572232934360940672962436849523915563328779942134504499568866135266628078485232098208237036724121481835035731201383423, 31221650155627849964466413749414700613823841060149524451234901677160009099014018926581094879840097248543411980533066831976617023676225625067854003317018794041723612556008471579060428898117790587991055681380408263382761841625714415879087478072771968160384909919958010983669368360788505288855946124159513118847747998656422521414980295212646675850690937883764000571667574381419144372824211798018586804674824564606122592483286575800685232128273820087791811663878057827386379787882962763290066072231248814920468264741654086011072638211075445447843691049847262485759393290853117072868406861840793895816215956869523289231421, 29944537515397953361520922774124192605524711306753835303703478890414163510777460559798334313021216389356251874917792007638299225821018849648520673813786772452822809546571129816310207232883239771324122884804993418958309460009406342872173189008449237959577469114158991202433476710581356243815713762802478454390273808377430685157110095496727966308001254107517967559384019734279861840997239176254236069001453544559786063915970071130087811123912044312219535513880663913831358790376650439083660611831156205113873793106880255882114422025746986403355066996567909581710647746463994280444700922867397754748628425967488232530303, 25703437855600135215185778453583925446912731661604054184163883272265503323016295700357253105301146726667897497435532579974951478354570415554221401778536104737296154316056314039449116386494323668483749833147800557403368489542273169489080222009368903993658498263905567516798684211462607069796613434661148186901892016282065916190920443378756167250809872483501712225782004396969996983057423942607174314132598421269169722518224478248836881076484639837343079324636997145199835034833367743079935361276149990997875905313642775214486046381368619638551892292787783137622261433528915269333426768947358552919740901860982679180791]
c =  [19131432661217908470262338421299691998526157790583544156741981238822158563988520225986915234570037383888112724408392918113942721994125505014727545946133307329781747600302829588248042922635714391033431930411180545085316438084317927348705241927570432757892985091396044950085462429575440060652967253845041398399648442340042970814415571904057667028157512971079384601724816308078631844480110201787343583073815186771790477712040051157180318804422120472007636722063989315320863580631330647116993819777750684150950416298085261478841177681677867236865666207391847046483954029213495373613490690687473081930148461830425717614569, 15341898433226638235160072029875733826956799982958107910250055958334922460202554924743144122170018355117452459472017133614642242411479849369061482860570279863692425621526056862808425135267608544855833358314071200687340442512856575278712986641573012456729402660597339609443771145347181268285050728925993518704899005416187250003304581230701444705157412790787027926810710998646191467130550713600765898234392350153965811595060656753711278308005193370936296124790772689433773414703645703910742193898471800081321469055211709339846392500706523670145259024267858368216902176489814789679472227343363035428541915118378163012031, 18715065071648040017967211297231106538139985087685358555650567057715550586464814763683688299037897182845007578571401359061213777645114414642903077003568155508465819628553747173244235936586812445440095450755154357646737087071605811984163416590278352605433362327949048243722556262979909488202442530307505819371594747936223835233586945423522256938701002370646382097846105014981763307729234675737702252155130837154876831885888669150418885088089324534892506199724486783446267336789872782137895552509353583305880144947714110009893134162185382309992604435664777436197587312317224862723813510974493087450281755452428746194446, 2282284561224858293138480447463319262474918847630148770112472703128549032592187797289965592615199709857879008271766433462032328498580340968871260189669707518557157836592424973257334362931639831072584824103123486522582531666152363874396482744561758133655406410364442174983227005501860927820871260711861008830120617056883514525798709601744088135999465598338635794275123149165498933580159945032363880613524921913023341209439657145962332213468573402863796920571812418200814817086234262280338221161622789516829363805084715652121739036183264026120868756523770196284142271849879003202190966150390061195469351716819539183797]
p_4=exCRT(c,n)
p=gmpy2.iroot(p_4,4)[0]
print(p)

注意中国剩余定理直接算出来的结果其实是p的4次方，要使用gmpy2.iroot()函数进行4次开方

第二步

我们要对ee2=3很敏感，低加密指数一般是个与坡口，我们再观察tmp和n的相对大小，我们发现tmp的3次方于n大小相等

已知

k*n+c*e*2=(e2+tmp)**3

那么就可以爆破k的大小来获取e2

import gmpy2
# gcd(e1,e2)=1
# 存在整数r，s使得re1 + se2 = 1(裴蜀定理)
ee1 = 42
ee2 = 3
ce1 = 
ce2 = 
tmp =  
n  =  
# assert(pow(e1,ee1,n)==ce1)
# assert(pow(e2+tmp,ee2,n)==ce2)
# c1 = m**e1 mod n
# c2 = m**e2 mod n
# (c1**r*c2**s) mod n = (m**(re1+se2)) mod n =m
# re1 + se2 = 1
for k in range(40000,45000):
    if(gmpy2.iroot(k*n+ce2,3)[0]==int(gmpy2.iroot(k*n+ce2,3)[0])):
        print(gmpy2.iroot(k*n+ce2,3)[0]-tmp)

按经验来说，e2一般不是一个太大的数，输出有很多，从正到负的都有，我们想要的就是输出刚刚从负到正的那个值

可得

1	e2=381791429275130

随后是解e1：

仔细观察可以发现ce1的值与n的值相差了数十个数量级，从概率统计的意义上讲，如果比n小的每个数作为结果的可能相同，那么这种事情发生的概率非常小，但是还有一种可能就是，由于e1很小，e1的42次方都比n小，从而导致模n没起效果。

我们试着给ce1开42次方，果然得到了一个差不多的整数，证实了猜想

1	e1=15218928658178

第三步

只给了e，n，c，这样一般是没办法直接得到明文的，这种情况下只能看看n可不可以用yafu分解，或者暴力分解

嗯，是可以的

那么此题的hint也成功解出来了

hint

emmmm，浪费表情

第四步

e与phi不互质

assert(c1==pow(flag,e1,p*q1))

assert(c2==pow(flag,e2,p*q2))

在这个条件中，c1,c2,e1,e1,p,q1,q2的数值我们都以及知道。于是对其先进行了一次常规的rsa公式计算，发现没有得到想要的flag。于是判断以下最大公约数：

x1=gmpy2.gcd(e1,p*q1)  =>14

x2=gmpy2.gcd(e2,p*q2)  =>14

我们发现在两个计算式中e和pq都不互素：(e1进行举例)

于是对  m^e1 = (m^14)^e1/14 =>(m^14)^   e1/(gcd(e1,p*q1))

c1=m^e1 mod p*q1       =(m^14)^   e1/(gcd(e2,p*q1))

c2=m^e2 mod p*q2       =(m^14)^   e2/(gcd(e2,p*q2))

=>

d1=imvert(e1//x1,p*q1)

d2=imvert(e2//x1,p*q2)

=>对得到的m1和m2的等式调换一下顺序

m^14=m1 mod p*q1

m^14=m2 mod p*q2

=>拆分

m^14=m1 mod p

m^14=m1 mod q1

m^14=m2 mod q2

=>通过gcd判断是否可以通过rsa求出d值

gcd(14,p-1)=14

gcd(14,q1-1)=2

gcd(14,q2-1)=2

=>所以我们选取下面两个式子进行运算

（m^2）^7=m1 mod q1

（m^2）^7=m2 mod q2

=>可以看作时另一个rsa进行求解，可解出

m^2=b1 mod q1

m^2=b2 mod q2

=>在此时刻，使用中国剩余定理求解m^2，再对其开方即可求得我们想要的flag

m=(b1*q1*gmpy2.invert(q2,q1)+b2*q2*gmpy2.invert(q1,q2))%(q1*q2)

q1 = 127587319253436643569312142058559706815497211661083866592534217079310497260365307426095661281103710042392775453866174657404985539066741684196020137840472950102380232067786400322600902938984916355631714439668326671310160916766472897536055371474076089779472372913037040153356437528808922911484049460342088834871
q2 =  114401188227479584680884046151299704656920536168767132916589182357583461053336386996123783294932566567773695426689447410311969456458574731187512974868297092638677515283584994416382872450167046416573472658841627690987228528798356894803559278308702635288537653192098514966089168123710854679638671424978221959513
c1 =  262739975753930281690942784321252339035906196846340713237510382364557685379543498765074448825799342194332681181129770046075018122033421983227887719610112028230603166527303021036386350781414447347150383783816869784006598225583375458609586450854602862569022571672049158809874763812834044257419199631217527367046624888837755311215081173386523806086783266198390289097231168172692326653657393522561741947951887577156666663584249108899327053951891486355179939770150550995812478327735917006194574412518819299303783243886962455399783601229227718787081785391010424030509937403600351414176138124705168002288620664809270046124
c2 =  7395591129228876649030819616685821899204832684995757724924450812977470787822266387122334722132760470911599176362617225218345404468270014548817267727669872896838106451520392806497466576907063295603746660003188440170919490157250829308173310715318925771643105064882620746171266499859049038016902162599261409050907140823352990750298239508355767238575709803167676810456559665476121149766947851911064706646506705397091626648713684511780456955453552020460909638016134124590438425738826828694773960514221910109473941451471431637903182205738738109429736425025621308300895473186381826756650667842656050416299166317372707709596
 
x1=gmpy2.gcd(e1,(p-1)*(q1-1))
x2=gmpy2.gcd(e2,(p-1)*(q2-1))
d1=gmpy2.invert(e1//x1,(p-1)*(q1-1))
d2=gmpy2.invert(e2//x2,(p-1)*(q2-1))
m1 = pow(c1,d1,p*q1)
m2 = pow(c2,d2,p*q2)
 
d1_ = gmpy2.invert(7,(q1-1)) 
d2_ = gmpy2.invert(7,(q2-1))
b1 = pow(m1,d1_,q1) 
b2 = pow(m2,d2_,q2)
m=(b1*q2*gmpy2.invert(q2,q1)+b2*q1*gmpy2.invert(q1,q2))%(q1*q2)
print(long_to_bytes(gmpy2.iroot(m,2)[0]))

总exp

import gmpy2
from Crypto.Util.number import long_to_bytes
 
n =  [20129615352491765499340112943188317180548761597861300847305827141510465619670536844634558246439230371658836928103063432870245707180355907194284861510906071265352409579441048101084995923962148527097370705452070577098780246282820065573711015664291991372085157016901209114191068574208680397710042842835940428451949500607613634682684113208766694028789275748528254287705759528498986306494267817198340658241873024800336013946294891687591013414935237821291805123285905335762719823771647853378892868896078424572232934360940672962436849523915563328779942134504499568866135266628078485232098208237036724121481835035731201383423, 31221650155627849964466413749414700613823841060149524451234901677160009099014018926581094879840097248543411980533066831976617023676225625067854003317018794041723612556008471579060428898117790587991055681380408263382761841625714415879087478072771968160384909919958010983669368360788505288855946124159513118847747998656422521414980295212646675850690937883764000571667574381419144372824211798018586804674824564606122592483286575800685232128273820087791811663878057827386379787882962763290066072231248814920468264741654086011072638211075445447843691049847262485759393290853117072868406861840793895816215956869523289231421 , 29944537515397953361520922774124192605524711306753835303703478890414163510777460559798334313021216389356251874917792007638299225821018849648520673813786772452822809546571129816310207232883239771324122884804993418958309460009406342872173189008449237959577469114158991202433476710581356243815713762802478454390273808377430685157110095496727966308001254107517967559384019734279861840997239176254236069001453544559786063915970071130087811123912044312219535513880663913831358790376650439083660611831156205113873793106880255882114422025746986403355066996567909581710647746463994280444700922867397754748628425967488232530303, 25703437855600135215185778453583925446912731661604054184163883272265503323016295700357253105301146726667897497435532579974951478354570415554221401778536104737296154316056314039449116386494323668483749833147800557403368489542273169489080222009368903993658498263905567516798684211462607069796613434661148186901892016282065916190920443378756167250809872483501712225782004396969996983057423942607174314132598421269169722518224478248836881076484639837343079324636997145199835034833367743079935361276149990997875905313642775214486046381368619638551892292787783137622261433528915269333426768947358552919740901860982679180791]
c =  [19131432661217908470262338421299691998526157790583544156741981238822158563988520225986915234570037383888112724408392918113942721994125505014727545946133307329781747600302829588248042922635714391033431930411180545085316438084317927348705241927570432757892985091396044950085462429575440060652967253845041398399648442340042970814415571904057667028157512971079384601724816308078631844480110201787343583073815186771790477712040051157180318804422120472007636722063989315320863580631330647116993819777750684150950416298085261478841177681677867236865666207391847046483954029213495373613490690687473081930148461830425717614569, 15341898433226638235160072029875733826956799982958107910250055958334922460202554924743144122170018355117452459472017133614642242411479849369061482860570279863692425621526056862808425135267608544855833358314071200687340442512856575278712986641573012456729402660597339609443771145347181268285050728925993518704899005416187250003304581230701444705157412790787027926810710998646191467130550713600765898234392350153965811595060656753711278308005193370936296124790772689433773414703645703910742193898471800081321469055211709339846392500706523670145259024267858368216902176489814789679472227343363035428541915118378163012031 , 18715065071648040017967211297231106538139985087685358555650567057715550586464814763683688299037897182845007578571401359061213777645114414642903077003568155508465819628553747173244235936586812445440095450755154357646737087071605811984163416590278352605433362327949048243722556262979909488202442530307505819371594747936223835233586945423522256938701002370646382097846105014981763307729234675737702252155130837154876831885888669150418885088089324534892506199724486783446267336789872782137895552509353583305880144947714110009893134162185382309992604435664777436197587312317224862723813510974493087450281755452428746194446, 2282284561224858293138480447463319262474918847630148770112472703128549032592187797289965592615199709857879008271766433462032328498580340968871260189669707518557157836592424973257334362931639831072584824103123486522582531666152363874396482744561758133655406410364442174983227005501860927820871260711861008830120617056883514525798709601744088135999465598338635794275123149165498933580159945032363880613524921913023341209439657145962332213468573402863796920571812418200814817086234262280338221161622789516829363805084715652121739036183264026120868756523770196284142271849879003202190966150390061195469351716819539183797]
sum_n = 1
rev_n = []
ni = []
m = 0
for i in n:
    sum_n = sum_n * i
for i in n:
    temp = sum_n//i
    ni.append(temp)
    rev_n.append(gmpy2.invert(temp,i))
for i in range(len(n)):
    m += c[i]*rev_n[i]*ni[i] % sum_n
p = gmpy2.iroot(m%sum_n,4)[0]
print(p)
 
 
 
ee1 = 42
ee2 = 3
ce1 =  45722651786340123946960815003059322528810481841378247280642868553607692149509126962872583037142461398806689489141741494974836882341505234255325683219092163052843461632338442529011502378931140356111756932712822516814023166068902569458299933391973504078898958921809723346229893913662577294963528318424676803942288386430172430880307619748186863890050113934573820505570928109017842647598266634344447182347849367714564686341871007505886728393751147033556889217604647355628557502208364412269944908011305064122941446516990168924709684092200183860653173856272384
ce2 =  13908468332333567158469136439932325992349696889129103935400760239319454409539725389747059213835238373047899198211128689374049729578146875309231962936554403287882999967840346216695208424582739777034261079550395918048421086843927009452479936045850799096750074359160775182238980989229190157551197830879877097703347301072427149474991803868325769967332356950863518504965486565464059770451458557744949735282131727956056279292800694203866167270268988437389945703117070604488999247750139568614939965885211276821987586882908159585863514561191905040244967655444219603287214405014887994238259270716355378069726760953320025828158
tmp =  864078778078609835167779565982540757684070450697854309005171742813414963447462554999012718960925081621571487444725528982424037419052194840720949809891134854871222612682162490991065015935449289960707882463387
n1  =  15911581555796798614711625288508309704791837516232122410440958830726078821069050404012820896260071751380436992710638364294658173571101596931605797509712839622479368850251206419748090059752427303611760004621378226431226983665746837779056271530181865648115862947527212787824629516204832313026456390047768174765687040950636530480549014401279054346098030395100387004111574278813749630986724706263655166289586230453975953773791945408589484679371854113457758157492241225180907090235116325034822993748409011554673180494306003272836905082473475046277554085737627846557240367696214081276345071055578169299060706794192776825039
def doit(ee,n,ce):
    k=0
    while True:
        x=ce+k*n
        if gmpy2.iroot(x,ee)[1]:
            return gmpy2.iroot(x,ee)[0]
        k=k+1
e1=doit(ee1,n1,ce1)
e2=doit(ee2,n1,ce2)-tmp
print(e1)
print(e2)
 
 
q1 = 127587319253436643569312142058559706815497211661083866592534217079310497260365307426095661281103710042392775453866174657404985539066741684196020137840472950102380232067786400322600902938984916355631714439668326671310160916766472897536055371474076089779472372913037040153356437528808922911484049460342088834871
q2 =  114401188227479584680884046151299704656920536168767132916589182357583461053336386996123783294932566567773695426689447410311969456458574731187512974868297092638677515283584994416382872450167046416573472658841627690987228528798356894803559278308702635288537653192098514966089168123710854679638671424978221959513
c1 =  262739975753930281690942784321252339035906196846340713237510382364557685379543498765074448825799342194332681181129770046075018122033421983227887719610112028230603166527303021036386350781414447347150383783816869784006598225583375458609586450854602862569022571672049158809874763812834044257419199631217527367046624888837755311215081173386523806086783266198390289097231168172692326653657393522561741947951887577156666663584249108899327053951891486355179939770150550995812478327735917006194574412518819299303783243886962455399783601229227718787081785391010424030509937403600351414176138124705168002288620664809270046124
c2 =  7395591129228876649030819616685821899204832684995757724924450812977470787822266387122334722132760470911599176362617225218345404468270014548817267727669872896838106451520392806497466576907063295603746660003188440170919490157250829308173310715318925771643105064882620746171266499859049038016902162599261409050907140823352990750298239508355767238575709803167676810456559665476121149766947851911064706646506705397091626648713684511780456955453552020460909638016134124590438425738826828694773960514221910109473941451471431637903182205738738109429736425025621308300895473186381826756650667842656050416299166317372707709596
 
x1=gmpy2.gcd(e1,(p-1)*(q1-1))
x2=gmpy2.gcd(e2,(p-1)*(q2-1))
d1=gmpy2.invert(e1//x1,(p-1)*(q1-1))
d2=gmpy2.invert(e2//x2,(p-1)*(q2-1))
m1 = pow(c1,d1,p*q1)
m2 = pow(c2,d2,p*q2)
 
d1_ = gmpy2.invert(7,(q1-1)) 
d2_ = gmpy2.invert(7,(q2-1))
b1 = pow(m1,d1_,q1) 
b2 = pow(m2,d2_,q2)
m=(b1*q2*gmpy2.invert(q2,q1)+b2*q1*gmpy2.invert(q1,q2))%(q1*q2)
print(long_to_bytes(gmpy2.iroot(m,2)[0]))

参考：

https://blog.csdn.net/shshss64/article/details/127403833

https://blog.csdn.net/a5555678744/article/details/117308377

[NPUCTF2020]共模攻击(共模攻击&Coppersmith定理)

hint

from gmpy2 import *
from Crypto.Util.number import *
from secret import hint

m = bytes_to_long(hint)
p = getPrime(256)
c = pow(m, 256, p)
print(p)

p, q = getPrime(256), getPrime(256)
n = p * q
e1, e2 = getPrime(32), getPrime(32)
c1, c2 = pow(c, e1, n), pow(c, e2, n)
print(n)
print(e1, c1)
print(e2, c2)


'''
107316975771284342108362954945096489708900302633734520943905283655283318535709
6807492006219935335233722232024809784434293293172317282814978688931711423939629682224374870233587969960713638310068784415474535033780772766171320461281579
2303413961 1754421169036191391717309256938035960912941109206872374826444526733030696056821731708193270151759843780894750696642659795452787547355043345348714129217723
2622163991 1613454015951555289711148366977297613624544025937559371784736059448454437652633847111272619248126613500028992813732842041018588707201458398726700828844249
'''

已知c1,c2,e1,e2,n，我们可以直接用共模攻击求出c，然后就是

c ≡ m^256^ mod n

我们需要求m，我们可以用sympy库中的nthroot_mod(c,e,n)函数 ,

nthroot_mod 主要用于在模运算下求解某个数的 n 次方根

from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext, invert
from sympy import nthroot_mod

p=107316975771284342108362954945096489708900302633734520943905283655283318535709
n=6807492006219935335233722232024809784434293293172317282814978688931711423939629682224374870233587969960713638310068784415474535033780772766171320461281579
e1=2303413961
e2=2622163991
c1=1754421169036191391717309256938035960912941109206872374826444526733030696056821731708193270151759843780894750696642659795452787547355043345348714129217723
c2=1613454015951555289711148366977297613624544025937559371784736059448454437652633847111272619248126613500028992813732842041018588707201458398726700828844249

s,s1,s2=gcdext(e1,e2)
c=(pow(c1,s1,n)*pow(c2,s2,n))%n
m=nthroot_mod(c,256,p)
print(long_to_bytes(m))

//b'm.bit_length() < 400'

我们知道了m的比特位少于400

我们来看task

from gmpy2 import *
from Crypto.Util.number import *
from secret import flag

flag = flag.strip(b"npuctf{").strip(b"}")
m = bytes_to_long(flag)

p, q = getPrime(512), getPrime(512)
n = p * q
e1, e2 = p, q
c1, c2 = pow(m, e1, n), pow(m, e2, n)

print(n)
print(c1)
print(c2)

'''
128205304743751985889679351195836799434324346996129753896234917982647254577214018524580290192396070591032007818847697193260130051396080104704981594190602854241936777324431673564677900773992273463534717009587530152480725448774018550562603894883079711995434332008363470321069097619786793617099517770260029108149
96860654235275202217368130195089839608037558388884522737500611121271571335123981588807994043800468529002147570655597610639680977780779494880330669466389788497046710319213376228391138021976388925171307760030058456934898771589435836261317283743951614505136840364638706914424433566782044926111639955612412134198
9566853166416448316408476072940703716510748416699965603380497338943730666656667456274146023583837768495637484138572090891246105018219222267465595710692705776272469703739932909158740030049375350999465338363044226512016686534246611049299981674236577960786526527933966681954486377462298197949323271904405241585
'''

塞个大佬博客

sage
a = 106427507401691650533776606268030543324548306805584488340881108460215302001780649045082140067384306297497785054794169701530927082798998717147796265177082494273319180022953309137549878052025764276170773098393102683446915458123682447310617265418188192465923366892572673596378919944244343124060963227516817375783
b = 926651656671911333597022401968870409343942400492881255142377951759176631494915016941991504123810265329862246592861145719213675502795378053564904818765377025096483601036025012267103260702787555612216755188521913405305861451125814149409508425602231670292131422273268728629782633354498648021859614223672123489318899205627785426402597996319440198218774038390809403281952702730883306007226797632389267386912707857093556335846269954270572920361347019614365402744026533713442449916555425678184406380167614011131702418493073759816310890056281917310110034453007210415242707924141697749818907383248545179118594511927630223830
n = 128205304743751985889679351195836799434324346996129753896234917982647254577214018524580290192396070591032007818847697193260130051396080104704981594190602854241936777324431673564677900773992273463534717009587530152480725448774018550562603894883079711995434332008363470321069097619786793617099517770260029108149

R.<x>=Zmod(n)[]
f = x^2 - a*x +b
f.small_roots(X=2^400)   #根的绝对边界，根就是flag

//4242839043019782000788118887372132807371568279472499477998758466224002905442227156537788110520335652385855

定义大数 a, b, 和 n： 这三个大数分别是多项式的系数和模数。你要解决的是一个二次多项式 f(x)=x2−a⋅x+bf(x) = x^2 - a \cdot x + bf(x)=x2−a⋅x+b，其中 aaa 和 bbb 是给定的大数，n 是模数。

SageMath 环境设置： R.<x> = Zmod(n)[] 这行代码的意思是：

Zmod(n) 表示在模 nnn 的有限域中进行计算。
R.<x> 创建了一个多项式环 R，并定义了 x 作为多项式中的变量。

这样，你就可以在模 nnn 上进行多项式运算了。

定义多项式 f： f = x^2 - a*x + b 定义了一个二次多项式 f(x)=x2−a⋅x+bf(x) = x^2 - a \cdot x + bf(x)=x2−a⋅x+b。这个多项式是你需要求根的对象。

查找小根： f.small_roots(X=2^400) 这行代码的作用是通过 small_roots 方法查找多项式 f(x) 在模 nnn 下的根。X=2^400 表示你希望在一个非常大的范围内查找根，具体范围为 24002^{400}2400，这是一个用于限制查找的参数。

small_roots 是一个算法，用来快速寻找多项式的根，特别是在给定模数时，能够有效地搜索出符合条件的“较小”的根。

最后转换

from Crypto.Util.number import long_to_bytes
m=4242839043019782000788118887372132807371568279472499477998758466224002905442227156537788110520335652385855
print(long_to_bytes(m))
//verrrrrrry_345yyyyyyy_rsaaaaaaa_righttttttt?

得到flag

[羊城杯 2020]RRRRRRRSA(wiener attack )

wiener attack 是依靠连分数进行的攻击方式，适用于非常接近某一值（比如1）时，求一个比例关系，通过该比例关系再来反推关键信息就简单很多。这种攻击对于解密指数d很小时有很好的效果，一般的用法是通过
ed mod phi(N)=1

得到 ed=k*phi(N)+1

即 e/phi(N)=k/d+1/phi(N)
这种情况下phi(N)≈N，且phi(N)非常大
所以有 e/N - k/d = 1/phi(N)，也就是说k/d与e/N非常接近，而e/N又是已知的
对e/N进行连分数展开，得到的一串分数的分母很有可能就是d（论文太难了，只能记结论了T_T），只要检验一下

ed mod phi(N)

看它是不是1就知道对不对了。

但是这道题倒是告诉我，wiener attack的利用并不一定是这样的方式，只要其他值符合类似的条件，也可以试着求出一个关键值。

另外注意：wiener attack使用是要满足一定数值条件的，对d和N的相对大小，以及p，q的相对大小都是有要求的

先看看题干，明显可以发现加密指数e非常大，有经验就晓得这和wiener attack脱不了干系。
代码的逻辑也很好理解，先是把flag分成两部分（其实两部分加密方式是一样的），然后生成两个非常接近的大素数P1，P2，然后生成了两个相邻的较小的大素数，用P1的平方和Q1相乘得到N1，N2同理。用两个相近巨大的加密指数E加密。

import hashlib
import sympy
from Crypto.Util.number import *

flag = 'GWHT{************}'

flag1 = flag[:19].encode()
flag2 = flag[19:].encode()
assert(len(flag) == 38)

P1 = getPrime(1038)
P2 = sympy.nextprime(P1)
assert(P2 - P1 < 1000)

Q1 = getPrime(512)
Q2 = sympy.nextprime(Q1)

N1 = P1 * P1 * Q1
N2 = P2 * P2 * Q2

E1 = getPrime(1024)
E2 = sympy.nextprime(E1)

m1 = bytes_to_long(flag1)
m2 = bytes_to_long(flag2)

c1 = pow(m1, E1, N1)
c2 = pow(m2, E2, N2)


output = open('secret', 'w')
output.write('N1=' + str(N1) + '\n')
output.write('c1=' + str(c1) + '\n')
output.write('E1=' + str(E1) + '\n')
output.write('N2=' + str(N2) + '\n')
output.write('c2=' + str(c2) + '\n')
output.write('E2=' + str(E2) + '\n')
output.close()
'''
N1=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1=55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2=39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
'''

但是和普通的wiener attack 不同的是，e与N并没有近到相除约为1的地步，相差还是很大的，也就是说解密指数d也许还是很大的，

这样就解不出来。

这道题有意思的部分就在于，e和N的关系不符合利用条件，但是N1和N2的关系却适合
对于这一道题:

N1/N2=(P1/P2)^2^ * (Q1/Q2)

显然我们可以知道的是N1/N2 <Q1/Q2所以在Q1/Q2在区间(N1/N2,1)之间 (这是关键）

尝试对N1/N2进行连分数展开并求其各项渐进分数，其中某个连分数的分母可能就是Q1（这个可以依靠N%Q来验证）

连分数生成

def continuedFra(x, y): #不断生成连分数的项
    cF = []
    while y:
        cF += [x // y]
        x, y = y, x % y
    return cF
def Simplify(ctnf): #化简
    numerator = 0
    denominator = 1
    for x in ctnf[::-1]: #注意这里是倒叙遍历
        numerator, denominator = denominator, x * denominator + numerator
    return (numerator, denominator) #把连分数分成分子和算出来的分母
def getit(c):
    cf=[]
    for i in range(1,len(c)):
        cf.append(Simplify(c[:i])) #各个阶段的连分数的分子和分母
    return cf #得到一串连分数

寻找合适的Q1

def wienerAttack(e, n):
    cf=continuedFra(e,n)
    for (Q2,Q1) in getit(cf):#遍历得到的连分数，令分子分母分别是Q2，Q1
        if Q1 == 0:
            continue
        if N1%Q1==0 and Q1!=1:#满足这个条件就找到了
            return Q1
    print('not find!')
Q1=wienerAttack(N1,N2)

最后的解密.

找到Q1后顺势就可以求出所有其他参数

from Crypto.Util.number import *
P1=gmpy2.iroot(N1//Q1,2)[0]
P2=gmpy2.next_prime(P1)
Q2=gmpy2.next_prime(Q1)
phi1=P1*(P1-1)*(Q1-1)
phi2=P2*(P2-1)*(Q2-1)
d1=gmpy2.invert(E1,phi1)
d2=gmpy2.invert(E2,phi2)
m1=long_to_bytes(gmpy2.powmod(c1,d1,N1))
m2=long_to_bytes(gmpy2.powmod(c2,d2,N2))
print((m1+m2))

[AFCTF2018]花开藏宝地

给了5个压缩包和提示

misc爷的事，直接叫个misc佬把压缩包解了

5个压缩包分别考的是数字爆破，小写字母爆破，大写字母爆破，无密码，ntfs流查看

每个压缩包里给了两组数据

我们解前三个压缩包，得到

x1 = 305345133911395218573790903508296238659147802274031796643017539011648802808763162902335644195648525375518941848430114497150082025133000033835083076541927530829557051524161069423494451667848236452337271862085346869364976989047180532167560796470067549915390773271207901537847213882479997325575278672917648417868759077150999044891099206133296336190476413164240995177077671480352739572539631359
m1 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820813413
x2 = 152012681270682340051690627924586232702552460810030322267827401771304907469802591861912921281833890613186317787813611372838066924894691892444503039545946728621696590087591246339208248647926966446848123290344911662916758039134817404720512465817867255277476717353439505243247568126193361558042940352204093381260402400739429050280526212446967632582771424597203000629197487733610187359662268583
m2 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820818553
x3 = 40952412095267791829743119118333311932687870987919948671780408726886151430242690997238831410249436653299224291445012397813221016909468630372862610415470277301591535416193017906909638241212666990959976187895288689640250810487806568164431359887246760313154046201720715301307811951233077581047872827004824833876458687145628724339714212107812941785880896399800008924818580623979723496070665230
m3 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820819351

所以，这个东西是什么。。？

了解了一个新的知识点，叫门限方案

参考：密码学协议举例（二）：秘密共享的门限方案 | Matrix67: The Aha Moments

门限方案也有很多种，参考：
Secret Sharing - Web Encrypt

所以y’即可通过对五组数据中任意三组使用中国剩余定理得到，p在题面中给出了,只需要用 y’mod p 即可得到flag

y1 = 305345133911395218573790903508296238659147802274031796643017539011648802808763162902335644195648525375518941848430114497150082025133000033835083076541927530829557051524161069423494451667848236452337271862085346869364976989047180532167560796470067549915390773271207901537847213882479997325575278672917648417868759077150999044891099206133296336190476413164240995177077671480352739572539631359
m1 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820813413

y2 = 152012681270682340051690627924586232702552460810030322267827401771304907469802591861912921281833890613186317787813611372838066924894691892444503039545946728621696590087591246339208248647926966446848123290344911662916758039134817404720512465817867255277476717353439505243247568126193361558042940352204093381260402400739429050280526212446967632582771424597203000629197487733610187359662268583
m2 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820818553

y3 = 40952412095267791829743119118333311932687870987919948671780408726886151430242690997238831410249436653299224291445012397813221016909468630372862610415470277301591535416193017906909638241212666990959976187895288689640250810487806568164431359887246760313154046201720715301307811951233077581047872827004824833876458687145628724339714212107812941785880896399800008924818580623979723496070665230
m3 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820819351

y4 = 100459779913520540098065407420629954816677926423356769524759072632219106155849450125185205557491138357760494272691949199099803239098119602186117878931534968435982565071570831032814288620974807498206233914826253433847572703407678712965098320122549759579566316372220959610814573945698083909575005303253205653244238542300266460559790606278310650849881421791081944960157781855164700773081375247
m4 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820820091

y5 = 230502064382947282343660159791611936696520807970361139469603458689311286041516767875903549263861950740778705012699983268093626403307298415066249636346303539570207577050391796770068203937723627361951969413683246596072925692670365490970847825269581004483964261491917680759091791653759514213188778401968676433284753781006738293752440186858616315727565803777032119737689210471541053061940547213
m5 = 347051559622463144539669950096658163425646411435797691973701513725701575100810446175849424000000075855070430240507732735393411493866540572679626172742301366146501862670272443070970511943485865887494229487420503750457974262802053722093905126235340380261828593508455621667309946361705530667957484731929151875527489478449361198648310684702574627199321092927111137398333029697068474762820822249

import libnum
from Crypto.Util.number import *
y = [y1,y2,y3]
c = [m1,m2,m3]
_m = libnum.solve_crt(y,c)
p = 80804238007977405688648566160504278593148666302626415149704905628622876270862865768337953835725801963142685182510812938072115996355782396318303927020705623120652014080032809421180400984242061592520733710243483947230962631945045134540159517488288781666622635328316972979183761952842010806304748313326215619695085380586052550443025074501971925005072999275628549710915357400946408857
m = _m % p
print(long_to_bytes(m))

from Crypto.Util.number import *
from secret import flag
m=bytes_to_long(flag)
p=getPrime(512)
q=getPrime(512)
print('p=',p)
print('q=',q)
n=p*q
e=65537
c=pow(m,e,n)
print('c=',c)
#p= 12408795636519868275579286477747181009018504169827579387457997229774738126230652970860811085539129972962189443268046963335610845404214331426857155412988073
#q= 12190036856294802286447270376342375357864587534233715766210874702670724440751066267168907565322961270655972226761426182258587581206888580394726683112820379
#c= 68960610962019321576894097705679955071402844421318149418040507036722717269530195000135979777852568744281930839319120003106023209276898286482202725287026853925179071583797231099755287410760748104635674307266042492611618076506037004587354018148812584502385622631122387857218023049204722123597067641896169655595

我们发现gcd(e,phi)=65537,e与phi不互质，但我们发现e与p-1互质

m = c ^ d mod n
==>
m = c ^ d mod p
m = c ^ d mod q
(注：此推论满足的前提是——在c不是p或q的倍数，以及d是正整数的情况下，m = c ^ d modp 和m = c ^ d modq 总是成立的，有兴趣的同志们可以自行查找推导过程，这里就不过多说了)

故有以下结论

1
2
3

故可以使用以下代码：
d = invert(e,p-1)
m = pow(c,d, p)

from Crypto.Util.number import *
import gmpy2

p= 12408795636519868275579286477747181009018504169827579387457997229774738126230652970860811085539129972962189443268046963335610845404214331426857155412988073
q= 12190036856294802286447270376342375357864587534233715766210874702670724440751066267168907565322961270655972226761426182258587581206888580394726683112820379
c= 68960610962019321576894097705679955071402844421318149418040507036722717269530195000135979777852568744281930839319120003106023209276898286482202725287026853925179071583797231099755287410760748104635674307266042492611618076506037004587354018148812584502385622631122387857218023049204722123597067641896169655595
e=65537
n = p * q
phi = (p-1)
print(gmpy2.gcd(e,phi))
d = gmpy2.invert(e,phi)
m = pow(c,d,p)
print(long_to_bytes(m))

RSA加密算法

rsa基本组成

已知p,q,e求d（rsa）

已知p,q,e,c 求明文m [buu rsarsa题]

已知p,q,dp,dq,c 求明文m [buu RSA1题]

已知e1,e2,c1,c2,n 求明文m(共模攻击）[buu RSA3]

已知e,n,dp,c 求明文m（dp泄露）[buu RSA2题]

已知p,q,e,n,文件加密密文 求密文m [buu RSA题]

已知p+q，(p+1)*(q+1),c,d求明文m（[GUET-CTF2019]BabyRSA ）

Dangerous RSA（低加密指数攻击）

RSAROLL（rsa）

rsa2

rsa5（低加密指数广播攻击）

[NCTF2019]childRSA(费马小定理)

[HDCTF2019]bbbbbbrsa

rsa4(低加密指数广播攻击)

[BJDCTF2020]rsa_output

[BJDCTF2020]RSA

[GWCTF 2019]BabyRSA(解方程)

SameMod（共模攻击）

[AFCTF2018]可怜的RSA（rsa公钥加密）

[RoarCTF2019]babyRSA(威尔逊定理)

分析

RSA & what（共模攻击&base64隐写）

[NPUCTF2020]EzRSA（最小公倍数(p,q) ∗ 最大公因数(p,q) = p∗q）

[MRCTF2020]babyRSA

[MRCTF2020]Easy_RSA

[HDCTF2019]together(base64与unicode之间的转换以及共模攻击)

[INSHack2017]rsa16m(低加密指数广播攻击)

[NPUCTF2020]认清形势，建立信心

[De1CTF2019]babyrsa(中国剩余定理&e与phi不互质&低加密&裴蜀定理)

第一步

第二步

第三步

第四步

总exp

[NPUCTF2020]共 模 攻 击(共模攻击&Coppersmith定理)

[羊城杯 2020]RRRRRRRSA(wiener attack )

[AFCTF2018]花开藏宝地

[MoeCTF2022]signin(e与phi不互质)

已知p,q,e,n,文件加密密文求密文m [buu RSA题]

[NPUCTF2020]共模攻击(共模攻击&Coppersmith定理)